
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,且AE=2,M为AD上一动点(不与A、D重合),AM=x,连结EM并延长交CD的延长线于F,过M作MG⊥EF交直线BC于点G,连结EG、FG.

(1)如图1,若M是AD的中点,求证:①△AEM≌△DFM;②△EFG是等腰三角形;
(2)如图2,当x为何值时,点G与点C重合?
(3)当x=3时,求△EFG的面积.
【答案】(1)证明见解析(2)当x=2或6时,点G与点C重合(3)![]()
【解析】试题分析:(1)①根据已知条件,利用ASA即可证得△AEM≌△DFM;②由△AEM≌△DFM可得EM=FM,又因MG⊥EF,根据线段垂直平分线的性质即可得EG=FG,结论得证;(2)当点G与点C重合时,易证△AEM∽△DMC,根据相似三角形的对应边成比例即可求得x值;(3)过G作GN⊥AD于N(如图3所示),证明△AEM∽△NMG,根据相似三角形的性质可求得MN=2AE=4,利用勾股定理求得EM的长,再证明△DMF∽△NGM,根据相似三角形的性质求得FM的长,进而的EF的长,根据△EFG的面积=![]() EFGM即可得结论.
EFGM即可得结论.
试题解析:
(1)证明:①∵四边形ABCD是矩形,
∴∠A=∠ADC=∠MDF=90°,
∵M是AD的中点,
∴AM=DM,
在△AEM和△DFM中,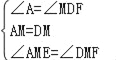 ,
,
∴△AEM≌△DFM(ASA);
②∵△AEM≌△DFM,
∴EM=FM,
又∵MG⊥EF,
∴EG=FG,
∴△EFG是等腰三角形;
(2)解:当点G与点C重合时,
∵∠A=∠EMC=∠ADC=90°,
∴∠AME+∠CMD=∠CMD+∠DCM,
∴∠AME=∠DCM,
∴△AEM∽△DMC,
∴![]() ,
,
∴![]() ,
,
解得:x1=2,x2=6,
∴当x=2或6时,点G与点C重合;
(3)解:过G作GN⊥AD于N,如图3所示:
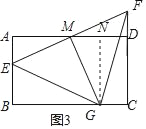
∴∠A=∠GNM=90°,GN=CD=6,
∴∠AME+∠NMG=∠NMG+∠NGM=90°,
∴∠AME=∠MGN,
∴△AEM∽△NMG,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∴MN=2AE=4,
由勾股定理得:EM=![]() =
=![]() =
=![]() ,
,
∴GM=2EM=2![]() ,
,
∵AB∥CD,
∴△DMF∽△NGM,
∴![]() =
=![]() ,
,
解得:MF=![]() ,
,
∴EF=EM+MF=![]() ,
,
∴△EFG的面积=![]() EFGM=
EFGM=![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.

(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
【答案】(1)5+3![]() ;(2)3.
;(2)3.
【解析】试题分析:(1)构造直角三角形,AB=![]() 且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
(2)先构造一个45°角,再利用面积是3,可画出图象.
试题解析:
(1)解:如图1所示:△ABC即为所求,
△ABC的周长为: ![]() +2
+2![]() +5=5+3
+5=5+3![]() ;
;

(2)解:如图2所示:△ABD中,∠ADB=45°,且面积为3.

【题型】解答题
【结束】
23
【题目】为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F,AB=6cm,AD=8cm.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.判断四边形FBGD的形状,并说明理由.
(3)在(2)的条件下,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,如图∠BAC=90°,BD平分∠ABC,点E在BC上,DE∥AB,点F在BC上,连结AF,∠C=36°.
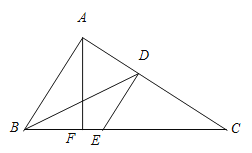
(1)求∠BDE的度数;
(2)若∠BAF∶∠CAF=2∶3,求证:AF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元.如果卖出相同数量的电脑,去年的销售额为10万元,那么今年的销售额只有8万元.
(1)今年三月份甲种型号电脑每台的售价为多少元?
(2)为增加收入,电脑公司决定经销乙种型号电脑.已知甲种型号电脑每台的进价为3500元,乙种型号电脑每台的进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台,则有几种进货方案?
(3)如果乙种型号电脑每台的售价为3800元,为打开乙种型号电脑的销路,公司决定每售出一台乙种型号电脑,返还顾客现金![]() 元,要使(2)中所有方案的获利相同,那么
元,要使(2)中所有方案的获利相同,那么![]() 的值应是多少?
的值应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42, ![]() =1.41】
=1.41】
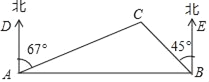
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com