
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元.如果卖出相同数量的电脑,去年的销售额为10万元,那么今年的销售额只有8万元.
(1)今年三月份甲种型号电脑每台的售价为多少元?
(2)为增加收入,电脑公司决定经销乙种型号电脑.已知甲种型号电脑每台的进价为3500元,乙种型号电脑每台的进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台,则有几种进货方案?
(3)如果乙种型号电脑每台的售价为3800元,为打开乙种型号电脑的销路,公司决定每售出一台乙种型号电脑,返还顾客现金![]() 元,要使(2)中所有方案的获利相同,那么
元,要使(2)中所有方案的获利相同,那么![]() 的值应是多少?
的值应是多少?
【答案】(1)今年三月份甲种型号电脑每台的售价为4000元;(2)共有5种进货方案;(3)当![]() =300时,(2)中所有方案的获利相同.
=300时,(2)中所有方案的获利相同.
【解析】
(1)根据销售的数量相等,则每台降低的价格乘以台数就是销售额减少的数量,即可列方程求解;
(2)根据销售额的范围即可列不等式组求得电脑台数的范围;
(3)把获利![]() 表示成台数y之间的函数,根据函数的性质求解.
表示成台数y之间的函数,根据函数的性质求解.
(1)设今年三月份甲种型号电脑每台的售价为![]() 元.
元.
根据题意,得![]() ,
,
解得![]()
经检验,![]() 是原方程的解.
是原方程的解.
∴今年三月份甲种型号电脑每台的售价为4000元
故答案为:今年三月份甲种型号电脑每台的售价为4000元
(2)设购进甲种型号电脑y台,则购进乙种型号电脑(15-y)台.
由题意得:48000≤3500y+3000(15-y)≤50000,
解得6≤y≤10
∴y的正整数解为6,7,8,9,10
∴共有5种进货方案
故答案为:共有5种进货方案
(3)设总获利为![]() 元,则
元,则![]() =(4 000-3500)y+(3800-3000-
=(4 000-3500)y+(3800-3000-![]() )(15-y)
)(15-y)
=(![]() -300)y+12000-15
-300)y+12000-15![]() ,
,
∴当![]() =300时,
=300时,![]() =12000-15
=12000-15![]() ,(2)中所有方案的获利相同.
,(2)中所有方案的获利相同.
故答案为:![]() =300
=300


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,点B,C分别在直线![]() 和
和![]() 上,点A,D是x轴上两点.
上,点A,D是x轴上两点.

(1)若此正方形边长为2,k=_______.
(2)若此正方形边长为a,k的值是否会发生变化?若不会发生变化,请说明理由;若会发生变化,求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,且AE=2,M为AD上一动点(不与A、D重合),AM=x,连结EM并延长交CD的延长线于F,过M作MG⊥EF交直线BC于点G,连结EG、FG.

(1)如图1,若M是AD的中点,求证:①△AEM≌△DFM;②△EFG是等腰三角形;
(2)如图2,当x为何值时,点G与点C重合?
(3)当x=3时,求△EFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=![]() ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.
(1)求直线l的表达式;
(2)若反比例函数![]() 的图象经过点P,求m的值.
的图象经过点P,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措.二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(生男生女机会均等,且与顺序有关).
(1)该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好是1男1女的概率;
(2)该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中至少有1个女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,CD交AF于G,
(1)如图1,若CF平分∠AFE,∠A=70°,求∠C;
(2)如图2,请写出∠A,∠C和∠AFC的数量关系并说明理由.
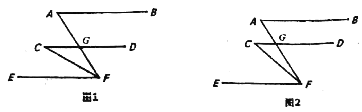
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com