
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.

【答案】详见解析
【解析】
(1)由角平分线定义可证△BCE≌△DCF(HL);(2)先证Rt△FAC≌Rt△EAC,得AF=AE,由(1)可得AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,![]()
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,![]() ,
,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F,AB=6cm,AD=8cm.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.判断四边形FBGD的形状,并说明理由.
(3)在(2)的条件下,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元.如果卖出相同数量的电脑,去年的销售额为10万元,那么今年的销售额只有8万元.
(1)今年三月份甲种型号电脑每台的售价为多少元?
(2)为增加收入,电脑公司决定经销乙种型号电脑.已知甲种型号电脑每台的进价为3500元,乙种型号电脑每台的进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台,则有几种进货方案?
(3)如果乙种型号电脑每台的售价为3800元,为打开乙种型号电脑的销路,公司决定每售出一台乙种型号电脑,返还顾客现金![]() 元,要使(2)中所有方案的获利相同,那么
元,要使(2)中所有方案的获利相同,那么![]() 的值应是多少?
的值应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42, ![]() =1.41】
=1.41】
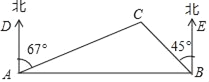
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
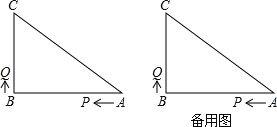
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=4,BC=6,∠ABC=60°,点P为ABCD内一点,点Q在BC边上,则PA+PD+PQ的最小值为( )
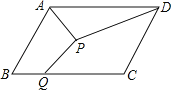
A.![]() B.6+2
B.6+2![]() C.5
C.5![]() D.10
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
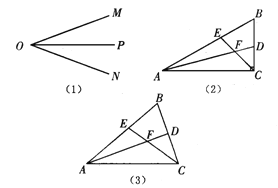
(1)如图(2),在△ABC中,∠ACB是直角,∠B=60°, AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图(3),在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(1)中所得结论是否仍然成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com