
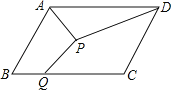
【题目】如图,在ABCD中,AB=4,BC=6,∠ABC=60°,点P为ABCD内一点,点Q在BC边上,则PA+PD+PQ的最小值为( )
A.![]() B.6+2
B.6+2![]() C.5
C.5![]() D.10
D.10
【答案】C
【解析】
如下图,将△APD绕点A逆时针旋转60°至△AFE处,通过边长转换,可将PA+PD+PQ转化为PF+EF+PQ的形式,再利根据两点之间线段最短,得出最小值.
如下图,将△APD绕点A逆时针旋转60°至△AFE处,连接FP,过点E作BC的垂线,交BC于点G,AD于点H,过点A作BC的垂线,交BC于点K
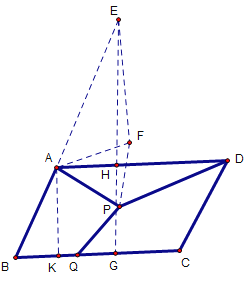
∵△AFE是△APD绕点A逆时针旋转60°得到
∴∠FAP=60°,∠EAD=60°,AF=AP,EF=PD
∴△APF是等边三角形,∴AP=PF
∴PA+PD+PQ=PF+FE+PQ≥EG
∵四边形ABCD是平行四边形,BC=6
∴AE=AD=BC=6,AD∥BC
∴在Rt△AHE中,AH=3,EH=3![]()
∵HG⊥BC,AK⊥BC,AD∥BC
∴AK⊥AD,GH⊥AD,∴AK=HG
∵∠ABC=60°,AB=4
∴在Rt△ABK中,BK=2,AK=2![]()
∴HG=2![]()
∴EG=3![]()
故选:C


科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,CD交AF于G,
(1)如图1,若CF平分∠AFE,∠A=70°,求∠C;
(2)如图2,请写出∠A,∠C和∠AFC的数量关系并说明理由.
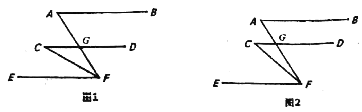
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件) | 购进所需费用(元) | ||
跳绳 | 足球 | ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)当AC、BC满足怎样的数量关系时,四边形AMCN是矩形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).

求(1)BF的长;
(2)EF的长 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com