
【题目】已知![]() ,求
,求![]() 的最大值与最小值.
的最大值与最小值.
【答案】x+y最大值为6,最小值为-3.
【解析】
先将|x+2|+|1-x|=9-|y-5|-|1+y|化为|x+2|+|1-x|+|y-5|+|1+y|=9.再对x、y的取值进行分类讨论:当x≥1,y≥5时;当1>x≥-2,5>y≥-1时;当x<-2,y<-1时.最后求出最大最小值.
|x+2|+|1-x|=9-|y-5|-|1+y|,
∴|x+2|+|1-x|+|y-5|+|1+y|=9,
当x≥1,y≥5时,x+2+x-1+y-5+y+1=9,
2x+2y=12 即x+y=6,
当1>x≥-2,5>y≥-1时,
x+2+1-x+5-y+y+1=9,但-3<x+y<6,
当x<-2,y<-1时,
-x-2+1-x+5-y-1-y=9,
得-2x-2y=6即 x+y=-3,
故x+y最大值为6,最小值为-3.


科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元.如果卖出相同数量的电脑,去年的销售额为10万元,那么今年的销售额只有8万元.
(1)今年三月份甲种型号电脑每台的售价为多少元?
(2)为增加收入,电脑公司决定经销乙种型号电脑.已知甲种型号电脑每台的进价为3500元,乙种型号电脑每台的进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台,则有几种进货方案?
(3)如果乙种型号电脑每台的售价为3800元,为打开乙种型号电脑的销路,公司决定每售出一台乙种型号电脑,返还顾客现金![]() 元,要使(2)中所有方案的获利相同,那么
元,要使(2)中所有方案的获利相同,那么![]() 的值应是多少?
的值应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
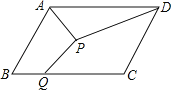
【题目】如图,在ABCD中,AB=4,BC=6,∠ABC=60°,点P为ABCD内一点,点Q在BC边上,则PA+PD+PQ的最小值为( )
A.![]() B.6+2
B.6+2![]() C.5
C.5![]() D.10
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.
(1)求乙队搬运量y与时间x之间的函数关系式.
(2)如果甲、乙两队各连续搬运5小时,那么乙队比甲队多搬运多少千克?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=x2﹣2mx+m2+![]() m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
(1)分别用含有m的代数式表示点A、B的坐标.
(2)判断点B能否落在y轴负半轴上,并说明理由.
(3)连结AC,设l=AC+BD,求l与m之间的函数关系式.
(4)过点A作y轴的垂线,交y轴于点P,以AP为边作正方形APMN,MN在AP上方,如图②,当正方形APMN与四边形ABCD重叠部分图形为四边形时,直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连结OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2.其中正确结论是_____;(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
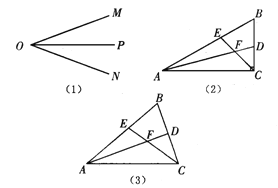
(1)如图(2),在△ABC中,∠ACB是直角,∠B=60°, AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图(3),在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(1)中所得结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣7.3)+5
(2)3﹣(﹣5)
(3)![]()
(4)(﹣12)÷(﹣![]() )
)
(5)4.7﹣(﹣8.9)﹣7.5+(﹣6)
(6)﹣3.5÷![]() ×|﹣
×|﹣![]() |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com