
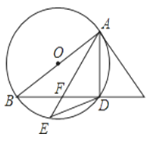
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由切线的性质得BA⊥AC,则∠2+∠BAD=90°,再根据圆周角定理得∠ADB=90°,则∠B+∠BAD=90°,所以∠B=∠2,接着由DA=DE得到∠1=∠E,由圆周角定理得∠B=∠E,所以∠1=∠2,可判断AF=AC,根据等腰三角形的性质得FD=DC;
(2)作DH⊥AE于H,如图,根据等腰三角形的性质得AH=EH=![]() AE=4,再根据勾股定理可计算出DH=3,然后证明△BDA∽△EHD,利用相似比可计算出AB=
AE=4,再根据勾股定理可计算出DH=3,然后证明△BDA∽△EHD,利用相似比可计算出AB=![]() ,从而可得⊙O的半径.
,从而可得⊙O的半径.
(1)证明:∵AC是⊙O的切线,
∴BA⊥AC,
∴∠2+∠BAD=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B=∠2,
∵DA=DE,
∴∠1=∠E,
而∠B=∠E,
∴∠B=∠1,
∴∠1=∠2,
∴AF=AC,
而AD⊥CF,
∴FD=DC;
(2)解:作DH⊥AE于H,如图,
∵DA=DE=5,
∴AH=EH=![]() AE=4,
AE=4,
在Rt△DEH中,DH= ![]() =3,
=3,
∵∠B=∠E,∠ADB=∠DHE=90°,
∴△BDA∽△EHD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
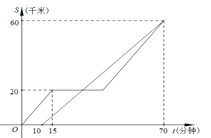
【题目】甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
(1)甲、乙两车行驶时的速度分别为多少?
(2)乙车出发多少分钟后第一次与甲车相遇?
(3)甲车中途因故障停止行驶的时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育运动学校准备在甲、已两位射箭选手中选出成绩比较稳定的一人参加集训,两人各射击了5箭,已知他们的总成绩(单位:环)相同,如下表所示:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)试求出表中a的值;
(2)请你通过计算,从平均数和方差的角度分析,谁将被选中.
[注:平均数x=![]() ;方差
;方差![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
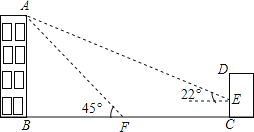
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
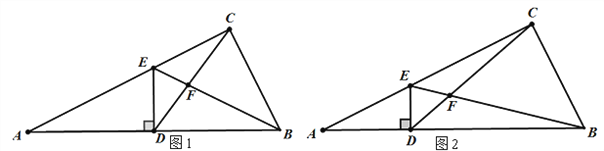
【题目】如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=![]() ,则
,则![]() =_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若
=_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若![]() ,tanA=
,tanA=![]() ,则
,则![]() =____.
=____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com