
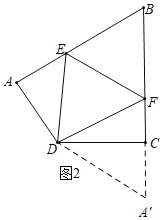
����Ŀ����ͼ�٣��ı���ABCDΪ�����Σ���E��F�ֱ���AB��BC�ϣ��ҡ�EDF=45������֤��AE+CF=EF������֤������
��1����ͼ�ڣ����ı���ABCD�У���ADC=120����DA=DC����DAB=��BCD=90������E��F�ֱ���AB��BC�ϣ��ҡ�EDF=60��������AE��CF��EF֮���������ϵ����֤����IJ��룻
��2����ͼ�ۣ����ı���ABCD�У���ADC=2����DA=DC����DAB���BCD��������E��F�ֱ���AB��BC�ϣ��ҡ�EDF=������ֱ��д��AE��CF��EF֮���������ϵ������֤����

���𰸡���1��AE+CF=EF��֤������������2��![]() �����ɼ�����.
�����ɼ�����.
��������
��1��������нس����̵���ʾ���ٽ�ϵڣ�1���ʵ�֤�����ۣ��ڵڶ��ʿ����ýس����̵ķ���������ȫ�ȣ��Ӷ��ﵽ֤�������
��2��ͬ���������ߣ�ͬ�����м��ɣ�ֱ��д�����룬��֤����
��1��ͼ2���룺AE+CF=EF��
֤������BC���ӳ����Ͻ�ȡCA'=AE������A'D��
�ߡ�DAB=��BCD=90����
���DAB=��DCA'=90����
�֡�AD=CD��AE=A'C��
���DAE�ա�DCA'��SAS����
��ED=A'D����ADE=��A'DC��
�ߡ�ADC=120����
���EDA'=120����
�ߡ�EDF=60����
���EDF=��A'DF=60����
��DF=DF��
���EDF�ա�A'DF��SAS����
��EF=A'F=FC+CA'=FC+AE��
��2����ͼ3��AE+CF=EF��

֤������BC���ӳ����Ͻ�ȡCA'=AE������A'D��
�ߡ�DAB���BCD��������BCD+��DCA'=180��
���DAB=��DCA'��
�֡�AD=CD��AE=A'C��
���DAE�ա�DCA'��SAS����
��ED=A'D����ADE=��A'DC��
�ߡ�ADC=2����
���EDA'=2����
�ߡ�EDF=����
���EDF=��A'DF=��
��DF=DF��
���EDF�ա�A'DF��SAS����
��EF=A'F=FC+CA'=FC+AE��


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����Ϊ1�������Σ�����һ���������������������Ҽ���������2��С�����Σ���ͼ�٣������У�3��������Χ�ɵ���������ֱ�������Σ��پ���һ��������������������4��С�����Σ���ͼ�ڣ���������˹��ɼ�������������ȥ�����������֦��Ҷï����������������2019�κ��γɵ�ͼ�������������ε�������ǣ�������

A.2018B.2019C.2020D.2021
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
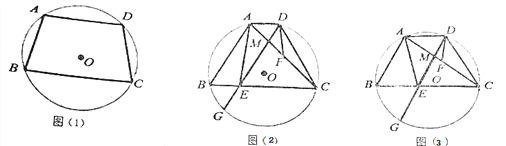
����Ŀ����ͼ,�ı���ABCD�ǡ�O���ڽ��ı���,AB=CD.
(1)��ͼ(1),��֤:AD��BC��
(2)��ͼ(2),��F��AC���е�,��DG��AB,��BC�ڵ�E,��AC�ڵ�M,��֤:AE=2DF��
(3)��(2)��������,��DGƽ�֡�ADC,GE=5![]() ,tan��ADF=4
,tan��ADF=4![]() ,���O�İ뾶��
,���O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() �IJ���ͼ����ͼ��ͼ����㣨��1��0�����Գ���Ϊֱ��
�IJ���ͼ����ͼ��ͼ����㣨��1��0�����Գ���Ϊֱ��![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ����
����![]() ���ܵ�
���ܵ�![]() ʱ��
ʱ�� ![]() ��
��![]() �����������������ȷ�Ľ����У����� ��
�����������������ȷ�Ľ����У����� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y=��x+4����ֱ��l��ȡ��B1����B1�ֱ���x�ᣬy�������ߣ���x����A1����y����C1��ʹ�ı���OA1B1C1Ϊ�����Σ���ֱ��l��ȡ��B2����B2�ֱ���x�ᣬA1B1�����ߣ���x����A2����A1B1��C2��ʹ�ı���A1A2B2C2Ϊ�����Σ����˷�����ֱ��l��˳��ȡ��B3��B4������Bn��������������A2A3B3C3��A3A4B4C4������An��1AnBnCn����A3������Ϊ___��B5������Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() ��x�������ύ��A��B���㣨A����B����ߣ�����AB=4��
��x�������ύ��A��B���㣨A����B����ߣ�����AB=4��
��1����kֵ��
��2������������ֱ��![]() ����C��D���㣬��S��ACD��
����C��D���㣬��S��ACD��
��3�������������Ƿ���ڲ�ͬ��A��ĵ�P��ʹS��PCD=S��ACD�������ڣ����P�����꣮
��4���������������е�P��ʹS��PCD=tS��ACD��������������������P����2����3����4��ʱ���ֱ�ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=��x2+2x+m��ͼ����x���һ������ΪA(3��0)����һ������ΪB������y�ύ�ڵ�C�����ö��κ���ͼ������һ��D(x��y)��ʹS��ABD=S��ABC����D�������Ϊ____________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н�����̣���֪![]() ��
��![]() ��
��![]() Ϊ��ABC�����ߣ�������
Ϊ��ABC�����ߣ�������![]() ��
��
���ж���ABC����״.
�⣺��![]() ���������������١�
���������������١�
��![]() �� ��
�� ��
��![]() ����������������������������������������������
����������������������������������������������
����ABCΪֱ��������.
�ʣ���1������������̣�����һ����ʼ���ִ�����д���ò��Ĵ���________��
����2�������ԭ����____________________________��
��3���������ȷ������_________________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ��ֱ�Ƕ���
��ֱ�Ƕ���![]() ��
��![]() ���ϣ�һ��Ƕ���
���ϣ�һ��Ƕ���![]() ��
��![]() ����.
����.

��1����ͼ1��ʾ����![]() ��������
��������![]() ����
����![]() ��������
��������![]() ����
����![]() ������.
������.
��2����ͼ2����![]() ��ǡ��ƽ��
��ǡ��ƽ��![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ��������������ϵ����˵������.
��������������ϵ����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com