
【题目】如图所示:![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,直角顶点
,直角顶点![]() 在
在![]() 轴上,一锐角顶点
轴上,一锐角顶点![]() 在
在![]() 轴上.
轴上.

(1)如图1所示,若![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,求,点
,求,点![]() 的坐标.
的坐标.
(2)如图2,若![]() 轴恰好平分
轴恰好平分![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,问
,问![]() 与
与![]() 有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.
【答案】(1)点![]() 坐标为
坐标为![]() ;(2)
;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)过点A作AD⊥OC,可证△ADC≌△COB,根据全等三角形对应边相等即可求出答案;
(2)延长BC、AE交于点F,可证△ACF≌△BCD,可证△ABE≌△FBE,即可求出BD=2AE.
解:(1)如图1,过点A作AD⊥x轴于D,
∵∠DAC+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠BCD=∠DAC
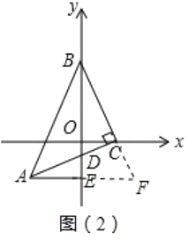
在△ADC和△COB中,
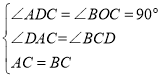
∴△ADC≌△COB(AAS)
∴AD=OC,CD=OB,
∴点B坐标为(0,4);
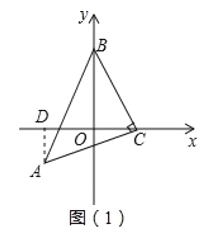
(2)如图2,延长BC,AE交于点F,
∵AC=BC,AC⊥BC
∴∠BAC=∠ABC=45°
∵BD平分∠ABC,
∴∠COD=22.5°,∠DAE=90°-∠ABD-∠BAD=22.5°,
在△ACF和△BCD中,
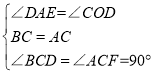
∴△ACF≌△BCD(ASA)
∴AF=BD
在△ABE和△FBE中

∴△ABE≌△FBE(ASA)
∴AE=EF
∴BD=2AE


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形ABCD中,AB=6,AD=8,点E为边AD上一点,将△ABE沿BE折叠后得到△BEF.

(1)如图1,若点E为AD的中点,延长BF交边CD于点G.
①求证:DG=FG.
②求FG的长度.
(2)如图2,若点E为边AD的一动点,连接FD,△DEF能否为直角三角形?若能,求出AE的值.若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:用3辆![]() 型车和2辆
型车和2辆![]() 型车载满货物一次可运货17吨;用2辆
型车载满货物一次可运货17吨;用2辆![]() 型车和3辆
型车和3辆![]() 型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用
型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.
(1)1辆![]() 型车和1辆
型车和1辆![]() 型车都载满货物一次可分别运货多少吨?
型车都载满货物一次可分别运货多少吨?
(2)若![]() 型车每辆需租金200元/次,
型车每辆需租金200元/次,![]() 型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许多代数恒等式可以借助图形的面积关系直观表达,如图①,根据图中面积关系可以得到:![]() 。
。

(1)如图②,根据图中面积关系,写出一个关于![]() 的等式 ;
的等式 ;
(2)利用(1)中的等式求解:![]() ,则
,则![]() ;
;
(3)小明用8个面积一样大的长方形(宽![]() ,长
,长![]() )拼图,拼出了如图甲、乙的两种图案;图案甲是一个大的正方形,中间阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求
)拼图,拼出了如图甲、乙的两种图案;图案甲是一个大的正方形,中间阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D 为∠BAC 的外角平分线上一点并且满足 BD=CD, 过 D 作 DE⊥AC 于 E,DF⊥AB 交 BA 的延长线于 F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.

(1)如图1,当点E在BC边的中点位置时,求证:AE=EM;
(2)如图2,当点E在BC边的任意位置时,(1)中的结论是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以每千克6元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价3元销售,全部售完。销售金额y(元)与销售量x(千克)之间的关系如图所示,请根据图象提供的信息完成下列问题:
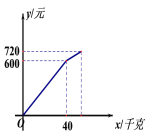
(1)降价前苹果的销售单价是 元/千克;
(2)求降价后销售金额y(元)与销售量x(千克)之间的函数表达式,并写出自变量的取值范围;
(3)该水果店这次销售苹果盈利了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com