
【题目】长方形ABCD中,AB=6,AD=8,点E为边AD上一点,将△ABE沿BE折叠后得到△BEF.

(1)如图1,若点E为AD的中点,延长BF交边CD于点G.
①求证:DG=FG.
②求FG的长度.
(2)如图2,若点E为边AD的一动点,连接FD,△DEF能否为直角三角形?若能,求出AE的值.若不能,请说明理由.
【答案】(1)①见解析;②![]() ;(2)3或6
;(2)3或6
【解析】
(1) ①连接EG,证明Rt△EGD≌Rt△EGF,即可解决问题;
②设DG=GF=x则GC=6-x,在Rt△BCG中利用勾股定理求解;
(2)需要分类讨论:当∠EFD=90°时,B,F,D共线,设AE=EF=x;
当∠FED=90°时,AE=AB=6.
解:(1)①证明:如图1中,连接EG,
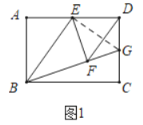
∵四边形ABCD是矩形,
∴∠A=∠EDG=90°,
∵EA=EF=ED,∠A=∠EFB=90°,
∴∠EFG=∠EDG=90°,
∵EG=EG,EF=ED,
∴Rt△EGD≌Rt△EGF(HL),
∴GD=GF.
②解:如图1中,设DG=GF=x则GC=6-x,
在Rt△BCG中,∵![]() =
=![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
∴GF=![]() .
.
(2)解:存在.如图2中,当∠EFD=90°时,B,F,D共线,设AE=EF=x,
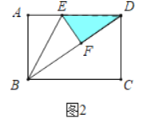
在Rt△ABD中,BD=10,
∵BF=BA=6,
∴DF=10-6=4
在Rt△EFD中,∵![]() ,
,
∴![]() ,
,
∴x=3,
∴AE=3.
如图3中,当∠FED=90°时,AE=AB=6.
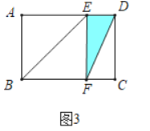
综上所述,满足条件的AE的值为3或6.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
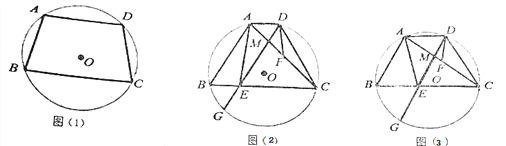
【题目】如图,四边形ABCD是⊙O的内接四边形,AB=CD.
(1)如图(1),求证:AD∥BC;
(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF;
(3)在(2)的条件下,若DG平分∠ADC,GE=5![]() ,tan∠ADF=4
,tan∠ADF=4![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.若该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,则D点的坐标为____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:已知![]() 、
、![]() 、
、![]() 为△ABC的三边,且满足
为△ABC的三边,且满足![]() ,
,
试判断△ABC的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.
设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):

(1)求y1的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)如果该公司销售人员小丽的月工资要超过1000元,那么小丽选用哪种方案最好?至少要销售商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,直角顶点
,直角顶点![]() 在
在![]() 轴上,一锐角顶点
轴上,一锐角顶点![]() 在
在![]() 轴上.
轴上.

(1)如图1所示,若![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,求,点
,求,点![]() 的坐标.
的坐标.
(2)如图2,若![]() 轴恰好平分
轴恰好平分![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,问
,问![]() 与
与![]() 有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形 ABCDE 中,∠A+∠B+∠E=α,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是( )

A. 90°+![]() α B.
α B. ![]() α﹣90° C.
α﹣90° C. ![]() α D. 540° -
α D. 540° -![]() α
α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com