
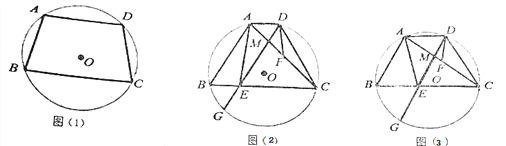
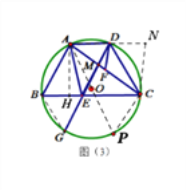
【题目】如图,四边形ABCD是⊙O的内接四边形,AB=CD.
(1)如图(1),求证:AD∥BC;
(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF;
(3)在(2)的条件下,若DG平分∠ADC,GE=5![]() ,tan∠ADF=4
,tan∠ADF=4![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接AC.由弦相等得到弧相等,进一步得到圆周角相等,即可得出结论.
(2)延长AD到N,使DN=AD,连接NC.得到四边形ABED是平行四边形,从而有AD=BE,DN=BE.由圆内接四边形的性质得到∠NDC=∠B.即可证明ΔABE≌ΔCND,得到AE=CN,再由三角形中位线的性质即可得出结论.
(3)连接BG,过点A作AH⊥BC,由(2)知∠AEB=∠ANC,四边形ABED是平行四边形,得到AB=DE.再证明ΔCDE是等边三角形,ΔBGE是等边三角形,通过解三角形ABE,得到AB,HB, AH,HE的长,由EC=DE=AB,得到HC的长.在Rt△AHC中,由勾股定理求出AC的长.
作直径AP,连接CP,通过解△APC即可得出结论.
试题解析:解:(1)连接AC.∵AB=CD,∴弧AB=弧CD,∴∠DAC=∠ACB,∴AD∥BC.
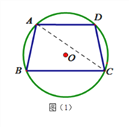
(2)延长AD到N,使DN=AD,连接NC.∵AD∥BC,DG∥AB,∴四边形ABED是平行四边形,∴AD=BE,∴DN=BE.∵ABCD是圆内接四边形,∴∠NDC=∠B.∵AB=CD,∴ΔABE≌ΔCND,∴AE=CN.∵DN=AD,AF=FC,∴DF=![]() CN,∴AE=2DF.
CN,∴AE=2DF.
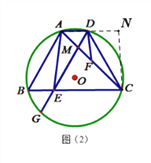
(3)连接BG,过点A作AH⊥BC,由(2)知∠AEB=∠ANC,四边形ABED是平行四边形,∴AB=DE.
∵DF∥CN,∴∠ADF=∠ANC,∴∠AEB=∠ADF,∴tan∠AEB= tan∠ADF=![]() ,DG平分∠ADC,∴∠ADG=∠CDG.∵AD∥BC,∴∠ADG=∠CED,∠NDC=∠DCE.∵∠ABC=∠NDC,∴∠ABC=∠DCE.∵AB∥DG,∴∠ABC=∠DEC,∴∠DEC=∠ECD=∠EDC,∴ΔCDE是等边三角形,∴AB=DE=CE.∵∠GBC=∠GDC=60°,∠G=∠DCB=60°,∴ΔBGE是等边三角形,BE= GE=
,DG平分∠ADC,∴∠ADG=∠CDG.∵AD∥BC,∴∠ADG=∠CED,∠NDC=∠DCE.∵∠ABC=∠NDC,∴∠ABC=∠DCE.∵AB∥DG,∴∠ABC=∠DEC,∴∠DEC=∠ECD=∠EDC,∴ΔCDE是等边三角形,∴AB=DE=CE.∵∠GBC=∠GDC=60°,∠G=∠DCB=60°,∴ΔBGE是等边三角形,BE= GE=![]() .∵tan∠AEB= tan∠ADF=
.∵tan∠AEB= tan∠ADF=![]() ,设HE=x,则AH=
,设HE=x,则AH= ![]() .∵∠ABE=∠DEC=60°,∴∠BAH=30°,∴BH=4x,AB=8x,∴4x+x=
.∵∠ABE=∠DEC=60°,∴∠BAH=30°,∴BH=4x,AB=8x,∴4x+x=![]() ,解得:x=
,解得:x=![]() ,∴AB=8
,∴AB=8![]() ,HB=4
,HB=4![]() , AH=12,EC=DE=AB=
, AH=12,EC=DE=AB=![]() ,∴HC=HE+EC=
,∴HC=HE+EC=![]() =
=![]() .在Rt△AHC中,AC=
.在Rt△AHC中,AC=![]() =
=![]() .
.
作直径AP,连接CP,∴∠ACP=90°,∠P=∠ABC=60°,∴sin∠P=![]() ,∴
,∴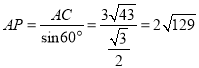 ,∴⊙O的半径是
,∴⊙O的半径是![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】小新家、小华家和书店依次在东风大街同一侧(忽略三者与东风大街的距离).小新小华两人同时各自从家出发沿东风大街匀速步行到书店买书,已知小新到达书店用了20分钟,小华的步行速度是40米/分,设小新、小华离小华家的距离分别为y1(米)、y2(米),两人离家后步行的时间为x(分),y1与x的函数图象如图所示,根据图象解决下列问题:
(1)小新的速度为_____米/分,a=_____;并在图中画出y2与x的函数图象
(2)求小新路过小华家后,y1与x之间的函数关系式.
(3)直接写出两人离小华家的距离相等时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图中提供的信息,解答下列问题:
分组 | 频数 | 频率 |
74.5≤x<79.5 | 2 | 0.04 |
79.5≤x<84.5 | a | 0.16 |
84.5≤x<89.5 | 20 | 0.40 |
89.5≤x<94.5 | 16 | 0.32 |
94.5≤x<100.5 | 4 | b |
合计 | 50 | 1 |
(1)频数、频率分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则![]()
=__(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,

(1)请你利用直尺和圆规完成如下操作:
①作△ABC的角平分线AD;
②作边AB的垂直平分线EF,EF与AD相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(2)线段PA,PB,PC之间的数量关系是 ;请说明理由.
(3)若∠ABC=70°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011内蒙古赤峰,7,3分)早晨,小张去公园晨练,下图是他离家的距离y(千
米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是 ( )

A.小张去时所用的时间多于回家所用的时间B.小张在公园锻炼了20分钟
C.小张去时的速度大于回家的速度 D.小张去时走上坡路,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.

(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形ABCD中,AB=6,AD=8,点E为边AD上一点,将△ABE沿BE折叠后得到△BEF.

(1)如图1,若点E为AD的中点,延长BF交边CD于点G.
①求证:DG=FG.
②求FG的长度.
(2)如图2,若点E为边AD的一动点,连接FD,△DEF能否为直角三角形?若能,求出AE的值.若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com