
【题目】若点A(3,3 )是正比例函数![]() 上一点,点M(m ,0)与点N(0 ,n)分别在x轴与y轴上,且∠MAN=90°.
上一点,点M(m ,0)与点N(0 ,n)分别在x轴与y轴上,且∠MAN=90°.
(1)如图1,当N点与原点O重合,求M点的坐标;
(2)如图2,已知m,n都为正数,连接MN,若MN=![]() ,求△MON的面积.
,求△MON的面积.

【答案】(1)M点坐标为(6,0);(2)![]()
【解析】试题分析:(1)过点A作AD⊥x轴于D,由点A的坐标即可得出AD=OD=3,进而得出∠AOD=∠OAD=45°,再通过角的计算得出∠AMO=45°,从而得出AO=AM,根据等腰三角形的性质即可得出OM=2OD,由此即可得出点M的坐标;(2)过点A作AQ⊥x轴于Q,作AP⊥y轴于P,由点A的坐标结合矩形的性质即可得出四边形APOQ是正方形,根据正方形的性质找出AP=AQ,再根据全等三角形的判定定理(ASA)即可证出△APN≌△AQM,从而得出PN=QM,通过边与边之间的关系结合勾股定理即可得出mn的值,将其代入三角形的面积公式即可得出结论.
试题解析:(1) 当N点与原点O重合时,如图作AD⊥x轴于D,
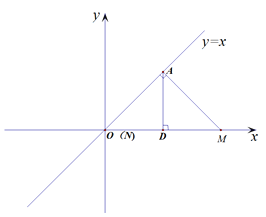
∵ A(3,3)
∴ AD=OD=3
∴ ∠AOD=∠OAD=45°
又∵∠MAN=90°
∴∠AMO=90°-45°=45°
∴ AO=AM,
∴OM=2OD=6
∴ M点坐标为(6,0)
(2)如图作AQ⊥![]() 轴于Q,AP⊥
轴于Q,AP⊥![]() 轴于P,
轴于P,
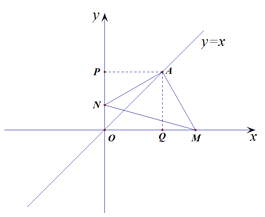
则 ∠APO=∠AQO=90°
又∵∠POQ=90°
∴ 四边形APOQ是矩形,
∵ A(3,3),
∴ OP=OQ=3,
∴ 四边形APOQ是正方形,
∴ AP=AQ.
∵ ∠PAN+∠NAQ=90°, ∠QAM+∠NAQ=90°,
∴ ∠PAN=∠QAM.
∴ △APN ≌ △AQM ,
∴ PN=QM.
∵M (m , 0), N (0 , n)
∴ ON=n,OM=m,
∴ PM=3-n,QM=m-3,
∴ 3-n=m-3,即![]() .
.
在Rt△MON中, ![]()
∴![]() ,即
,即![]()
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是( )
A.47B.48C.48.5D.49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近似数3.27的准确值a的取值范围是( )
A.3.265≤a<3.275
B.3.265<a<3.275
C.3.265≤a≤3.274
D.3.265<a≤3.275
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DB∥FG∥EC,A是FG上一点,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
(1)请你求出∠BAC的度数;
(2)请你求出∠PAG的度数.
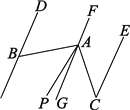
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
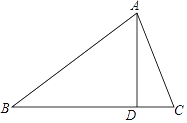
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16
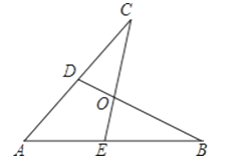
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( ) 
A.4.5
B.5
C.5.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形,是因式分解的是( )
A. x(x-1)=x2-x B. x2-x+1 = x(x-1)+1
C. x2-x =" x(x-1)" D. 2a(b+c)=2ab+2ac
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com