
(本题10分)如图,△ABC中,AB=AC,D、E、F分别在BC、AB、AC上,且BE=CD,BD=CF.
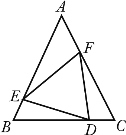
(1)求证:DE=DF;
(2)当∠A的度数为多少时,△DEF是等边三角形,并说明理由.
(1)证明详见解析;(2)∠A=60°.
【解析】
试题分析:(1)通过证明△BDE和 △CFD全等得到DE=DF;
(2)利用三角形全等的性质及等式的性质证得∠EDF=∠C,当∠A=60°时,∠B=∠C =60°,此时∠EDF=∠C=60°,所以△DEF是等边三角形.
试题解析:证明:(1)∵AB=AC,
∴ ∠B=∠C,
在△BDE和 △CFD 中,
 ,
,
∴ △BDE≌ △CFD(SAS).
∴DE=DF;
(2)当∠A=60°时, △DEF是等边三角形.
理由:∵ △BDE≌ △CFD,
∴∠BDE=∠CFD,
∵∠BDE+∠EDF=∠CFD+∠C,
∴∠EDF=∠C,
又∵DE=DF,要使△DEF是等边三角形,只要∠EDF=60°,
则∠C=∠EDF=60°,
∴当∠A=60°时,∠B=∠C =60°,此时△DEF是等边三角形.
考点:全等三角形的判定和性质;等边三角形的判定.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源:2014-2015学年江苏省滨海县七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,已知 ∥
∥ ,∠1=3∠2,∠2=25°,求
,∠1=3∠2,∠2=25°,求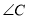 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省滨海县八年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图所示,在边长为1个单位的小正方形网格中,△AOB的顶点均在格点上,A(1,3),B(3,2).
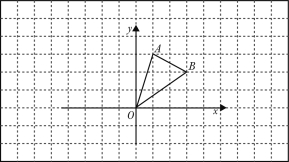
(1)B点关于y对称的点的坐标为 ;
(2)将△AOB向左平移3个单位长度得到△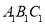 ,请画出△
,请画出△ ;
;
(3)在(2)的条件下,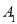 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
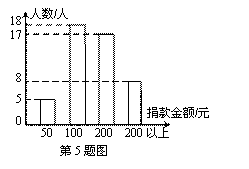
云南鲁甸发生地震后,某社区开展献爱心活动,社区党员积极向灾区捐款,如图是该社区部分党员捐款情况的条形统计图,那么本次捐款钱数的众数和中位数分别是
A.100元,100元 B.100元,200元 C.200元,100元 D.200元,200元
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com