已知关于x的一元二次方程mx2﹣(m+2)x+2=0． (1)证明:不论m为何值时.方程总有实数根, (2)m为何整数时.方程有两个不相等的正整数根．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

已知关于x的一元二次方程mx²﹣（m+2）x+2=0．

（1）证明：不论m为何值时，方程总有实数根；

（2）m为何整数时，方程有两个不相等的正整数根．

解：（1）△=（m+2）²﹣8m

=m²﹣4m+4

=（m﹣2）²，

∵不论m为何值时，（m﹣2）²≥0，

∴△≥0，

∴方程总有实数根；

（2）解方程得，x=，

x₁=，x₂=1，

∵方程有两个不相等的正整数根，

∴m=1或2，m=2不合题意，

∴m=1．

练习册系列答案

口算题卡加应用题专项沈阳出版社系列答案

名师伴你成长课时同步学练测系列答案

优品全程特训卷系列答案

小学单元期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：2014-2015学年江苏省滨海县八年级上学期期末考试数学试卷（解析版） 题型：解答题

(本题10分)如图，△ABC中，AB＝AC，D、E、F分别在BC、AB、AC上，且BE＝CD，BD＝CF．

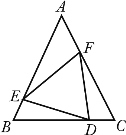
（1）求证：DE＝DF；

（2）当∠A的度数为多少时，△DEF是等边三角形，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

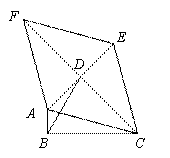
定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径，即损矩形外接圆的直径．

如图，△ABC中，∠ABC=90º，以AC为一边向形外作菱形ACEF，点D是菱形ACEF对角线的交点，连接BD，若∠DBC=60º，∠ACB=15º，BD=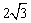，则菱形ACEF的面积为．

查看答案和解析>>

科目：初中数学 来源： 题型：

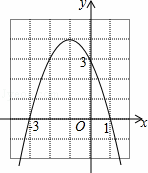
如图是二次函数y=ax²+bx+c的图象，下列结论：

①二次三项式ax²+bx+c的最大值为4；

②4a+2b+c＜0；

③一元二次方程ax²+bx+c=1的两根之和为﹣1；

④使y≤3成立的x的取值范围是x≥0．

其中正确的个数有（　　）

查看答案和解析>>

科目：初中数学 来源： 题型：

古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为a₁，第二个三角数记为a₂…，第n个三角数记为a_n，计算a₁+a₂，a₂+a₃，a₃+a₄，…由此推算a₃₉₉+a₄₀₀=　

查看答案和解析>>

科目：初中数学 来源： 题型：

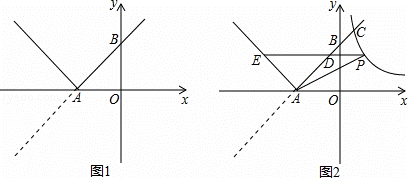
如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）．

（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；

（2）如图2，双曲线y=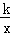与新函数的图象交于点C（1，a），点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．

①试求△PAD的面积的最大值；

②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判断△ABC∽△AED的是（　　）

A．

∠AED=∠B

B．

∠ADE=∠C

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：

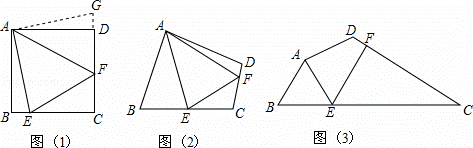
问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．

【发现证明】

小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．

【类比引申】

如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足　　关系时，仍有EF=BE+FD．

【探究应用】

如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40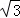（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据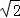：=1.41，=1.73）