
【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
【答案】(1)8,12;(2)t=4或者t=![]() ;(3)当t=6时,PQ+MN最小值为10.
;(3)当t=6时,PQ+MN最小值为10.
【解析】
(1)根据绝对值和平方的非负性即可得出a+8=0,b﹣12=0,从而求出线段OA、OB的长;
(2)题干给出了数轴上两点距离的表示方式,因此要求出t的值,只需要表示出AN=2AM,则将方程接出即可;
(3)首先根据中点公式表示出P、Q两点,然后表示出PQ+MN,再根据t的范围去掉绝对值,最后就可以求出PQ+MN的最小值.
解:(1)∵|a+8|+(b﹣12)2=0,
∴a+8=0,b﹣12=0,
∴a=﹣8,b=12,
∵点A、B在数轴上对应的数为a、b,
∴OA=8,OB=12,
故答案为:8,12;
(2)根据题意得:M点表示的数为:﹣t,N点表示的数为:12﹣3t,
则:AM=|8﹣t|,AN=|20﹣3t|,
∵AN=2AM,
∴|20﹣3t|=2|8﹣t|,
则(20﹣3t)=±2(8﹣t),
解得:t=4或者t=![]() ;
;
(3)∵点P为线段AM的中点,则P点表示的数为:![]() ,
,
∵Q为线段BN的中点,Q点表示的数为:![]() ,
,
∴PQ=![]() =|t﹣16|,
=|t﹣16|,
MN=|2t﹣12|,
∴PQ+MN=|t﹣16|+|2t﹣12|,
当t≥16时,原式=t﹣16+2t﹣12=3t﹣28;此时当t=16时最小值为20,
当6≤t≤16时,原式=16﹣t+2t﹣12=t+4;此时当t=6时最小值为10,
当t≤6时,原式=16﹣t+12﹣t=28﹣3t;此时当t=6时最小值为10,
综上所述当t=6时,PQ+MN最小值为10.


科目:初中数学 来源: 题型:
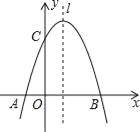
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形AECF中,![]() .CE、CF分别是△ABC的内,外角平分线.
.CE、CF分别是△ABC的内,外角平分线.

(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
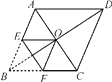
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
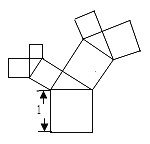
A.1B.2018C.2019D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
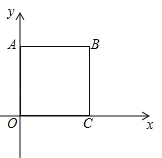
【题目】如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1: ![]() , 点A的坐标为(0,1),则点E的坐标是________或________.
, 点A的坐标为(0,1),则点E的坐标是________或________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为 ;
),则以AB为边的“坐标菱形”的最小内角为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
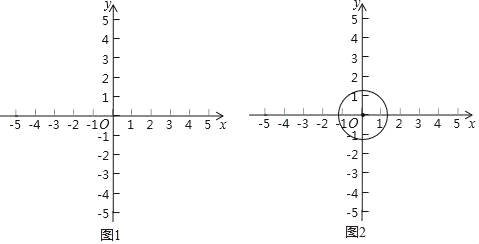
(3)⊙O的半径为![]() ,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com