
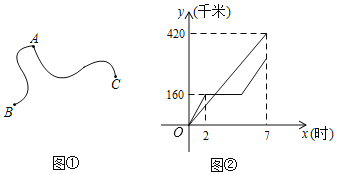
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
【答案】(1)3小时;(2)y=80x﹣240;(3)当x为![]() 或
或![]() 时,两车与A 地的距离恰好相同
时,两车与A 地的距离恰好相同
【解析】
(1)根据题意和图象中的数据可以求得甲车到达B地休息了多长时间;
(2)根据函数图象中的数据利用待定系数法可以求得甲车返回A地途中y与x之间的函数关系式;
(3)根据函数图象中的数据可以求得甲、乙的速度,根据甲、乙两车所在的位置分类讨论,分别列出对应的方程,从而可以解答本题.
解:(1)由题意可得,
甲车到达B地休息了:7﹣2﹣2=3(小时),
故答案为:3小时;
(2)设 甲车返回A地途中y与x之间的函数关系式是y=kx+b,
将(2+3,160)和(7,320)代入,得
![]() ,
,
得![]() ,
,
即甲车返回A地途中y与x之间的函数关系式是y=80x﹣240;
(3)甲车的速度为160÷2=80km/h,
乙车的速度为:420÷7=60km/h,
A、C两地的距离为420÷2=210
∴甲车到达点C需要210÷60=![]() 小时
小时
当0<x≤2时,
∵甲车速度>乙车速度
∴此时不存在x,使两车与A地的路程恰好相同;
当2<x≤![]() 时,此时甲车休息,距A地160千米,而乙车还未到C地
时,此时甲车休息,距A地160千米,而乙车还未到C地
∴60x=160,得x=![]() ;
;
当![]() <x≤5时,此时甲车休息,距A地160千米,而乙车从C地返回
<x≤5时,此时甲车休息,距A地160千米,而乙车从C地返回
∴420-60x=160,
得x=![]() ;
;
当5<x<7时,
根据甲、乙两车同时返回到A地,而题中要求不考虑两车同在A地的情况
此时不存在x,使两车与A地的路程恰好相同.
综上所述:当x为![]() 或
或![]() 时,两车与A 地的距离恰好相同.
时,两车与A 地的距离恰好相同.


科目:初中数学 来源: 题型:
【题目】如图,在坡顶![]() 处的同一水平面上有一座古塔
处的同一水平面上有一座古塔![]() ,数学兴趣小组的同学在斜坡底
,数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求古塔
.求古塔![]() 的高度.(结果精确到
的高度.(结果精确到![]() 米,参考数据:
米,参考数据: ![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
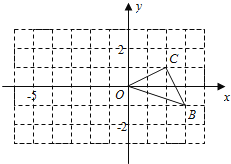
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
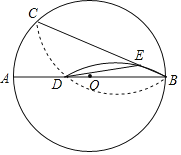
【题目】如图,将⊙O上的![]() 沿弦BC翻折交半径OA于点D,再将
沿弦BC翻折交半径OA于点D,再将![]() 沿BD翻折交BC于点E,连结DE.若AB=10,OD=1,则线段DE的长为( )
沿BD翻折交BC于点E,连结DE.若AB=10,OD=1,则线段DE的长为( )
A.5B.2![]() C.2
C.2![]() D.
D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
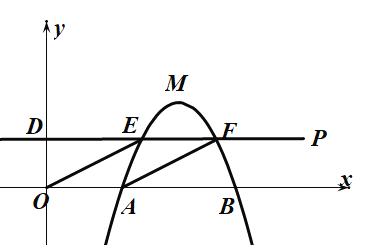
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(2,0),B(5,0),过点D(0,![]() )作y轴的垂线DP交图象于E、F.
)作y轴的垂线DP交图象于E、F.
(1)求b、c的值和抛物线的顶点M的坐标;
(2)求证:四边形OAFE是平行四边形;
(3)将抛物线向左平移的过程中,抛物线的顶点记为M′,直线DP与抛物线的左交点为E′,连接OM′,OE′,当OE′+OM′的值最小时求直线OE′的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
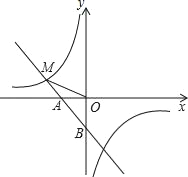
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
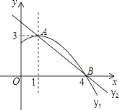
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 、
、![]() 是圆
是圆![]() 中的两条弦,连接
中的两条弦,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
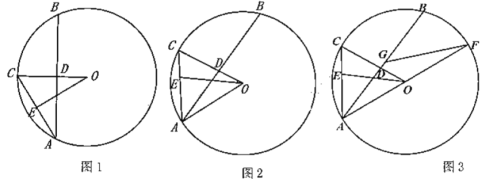
(1)如图1,若![]() ,求证:弧
,求证:弧![]()
![]() 弧
弧![]() ;
;
(2)如图2,连接![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在第(2)问的条件下,延长![]() 交圆
交圆![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
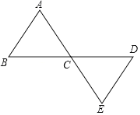
【题目】如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2018cm后,它停在了点_____上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com