
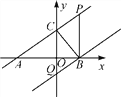
【题目】如图,若直线y=![]() x+2分别交x轴、y轴于A,C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
x+2分别交x轴、y轴于A,C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
(1)求点B和点P的坐标;
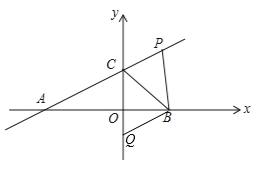
(2)过点B作直线BQ∥AP,交y轴于点Q,求点Q的坐标和四边形BPCQ的面积.
【答案】(1)B(2,0),P(2,3);(2)6.
【解析】试题分析:(1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,根据S△ABC=6可求出点B的坐标,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(2)由PB⊥x轴可得出PB∥CQ,结合BQ∥AP可得出四边形BPCQ为平行四边形,再根据点B、C、P的坐标即可得出点Q的坐标以及四边形BPCQ的面积.
试题解析:解:(1)当x=0时,y=![]() x+2=2,∴点C的坐标为(0,2);
x+2=2,∴点C的坐标为(0,2);
当y=![]() x+2=0时,x=﹣4,∴点A的坐标为(﹣4,0).
x+2=0时,x=﹣4,∴点A的坐标为(﹣4,0).
设点B的坐标为(m,0),则S△ABC=![]() ABOC=
ABOC=![]() ×[m﹣(﹣4)]×2=6,解得:m=2,点B的坐标为(2,0).当x=2时,y=
×[m﹣(﹣4)]×2=6,解得:m=2,点B的坐标为(2,0).当x=2时,y=![]() x+2=3,∴点P的坐标为(2,3).
x+2=3,∴点P的坐标为(2,3).
(2)∵PB⊥x轴,∴PB∥CQ.∵BQ∥AP,∴四边形BPCQ为平行四边形.∵点C(0,2),点B(2,0),点P(2,3),∴点Q的坐标为(0,﹣1),∴S平行四边形BPCQ=OBBP=2×3=6.


科目:初中数学 来源: 题型:
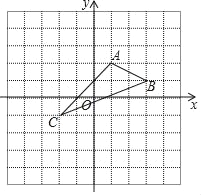
【题目】如图所示,
(1)写出顶点C的坐标;
(2)作△ABC关于y轴对称的△A1B1C1,并写出B1的坐标;
(3)若点A2(a,b)与点A关于x轴对称,求a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(a+8)x+(6-b).
(1)a,b为何值时,y随x的增大而增大?
(2)a,b为何值时,图象过第一、二、四象限?
(3)a,b为何值时,图象与y轴的交点在x轴上方?
(4)a,b为何值时,图象过原点?
查看答案和解析>>
科目:初中数学 来源: 题型:
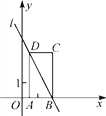
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(![]() ,0),B(2,0),直线l:y=kx+a经过B,D两点.
,0),B(2,0),直线l:y=kx+a经过B,D两点.
(1)求直线l的解析式;
(2)将直线l平移得到直线y=kx+b,若它与矩形有公共点,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在班级体锻课上,有三名同学站在△ABC的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个凳子,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边上高的交点 D. 三边垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6.M、N分别是AB、CD边的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,自来水公司对水价作出规定:当用水量不超过10吨时,每吨收费1.2元;当超过10吨时,超过部分每吨收费1.5元.某个月一户居民交费18元,则这户居民这个月用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com