
【题目】已知一次函数y=(a+8)x+(6-b).
(1)a,b为何值时,y随x的增大而增大?
(2)a,b为何值时,图象过第一、二、四象限?
(3)a,b为何值时,图象与y轴的交点在x轴上方?
(4)a,b为何值时,图象过原点?
【答案】(1)a>-8,b为全体实数;(2)a<-8,b<6;(3)a≠-8,b<6;(4)a≠-8,b=6.
【解析】(1)由y随x的增大而增大,利用一次函数的性质可得出结论;
(2)由一次函数图象过第一、二、四象限,利用一次函数图象与系数的关系可得出结论;
(3)根据一次函数的定义结合一次函数图象上点的坐标特征,得到a+8≠0,6-b>0,解之即可得出结论;
(4)根据一次函数的定义结合一次函数图象上点的坐标特征,得到a+8≠0,6-b=0,解之即可得出结论.
试题解析:解:(1)∵y随x的增大而增大,∴a+8>0,解得:a>-8,∴当a>-8,b为全体实数时,y随x的增大而增大;
(2)∵一次函数y=(a+8)x+(6-b)的图象过第一、二、四象限,∴![]() ,解得:a<-8且b<6,∴当a<-8且b<6时,一次函数y=(a+8)x+(6-b)的图象过第一、二、四象限;
,解得:a<-8且b<6,∴当a<-8且b<6时,一次函数y=(a+8)x+(6-b)的图象过第一、二、四象限;
(3)∵一次函数y=(a+8)x+(6-b)的图象与y轴的交点在x轴上方,∴a+8≠0,6-b>0,解得:a≠-8,b<6,∴当a≠-8且b<6时,一次函数y=(a+8)x+(6-b)的图象与y轴的交点在x轴上方;
(4)∵一次函数y=(a+8)x+(6-b)的图象过原点,∴a+8≠0,6-b=0,解得:a≠-8,b=6,∴当a≠-8且b=6时,一次函数y=(a+8)x+(6-b)的图象过原点.


科目:初中数学 来源: 题型:
【题目】舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )
A. 4.995×1011 B. 49.95×1010 C. 0.4995×1011 D. 4.995×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x+m)(x2-3x+n)的展开式中不含x2和x项,则m,n的值分别为( )
A. m=3,n=1 B. m=3,n=-9 C. m=3,n=9 D. m=-3,n=9
查看答案和解析>>
科目:初中数学 来源: 题型:
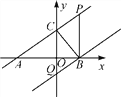
【题目】如图,若直线y=![]() x+2分别交x轴、y轴于A,C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
x+2分别交x轴、y轴于A,C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
(1)求点B和点P的坐标;
(2)过点B作直线BQ∥AP,交y轴于点Q,求点Q的坐标和四边形BPCQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好营造班级的学习氛围,某中学对九年级六个班有关中考备考宣传墙报进行评比,评分如下:
班级 | 九(1) | 九(2) | 九(3) | 九(4) | 九(5) | 九(6) |
得分 | 95 | 94 | 91 | 90 | 88 | 88 |
(1)求出各班得分的极差、众数、平均数;
(2)本次评比设一、二、三奖,各班均能获奖,具体要求:一等奖的得分>二等奖的得分>三等奖的得分,一等奖的名额不能超过2个,三等奖的名额不能少于2个。若从上述方案中任选一种进行评奖,用列举法求出九(3)班获二等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com