【题目】已知正比例函数y=kx（k≠0）的函数值y随x的增大而减小，则一次函数y=x+k的图象大致是（ ）
A.
B.
C.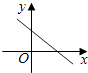
D.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系，现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度． 
水银柱的长度x（cm） | 4.0 | … | 8.0 | 9.6 |
体温计的度数y（℃） | 35.0 | … | 40.0 | 42.0 |
（1）求y关于x的函数关系式（不需要写出函数自变量x的取值范围）；
（2）用该体温计测体温时，水银柱的长度为6.0cm，求此时体温计的读数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2+2bx+c（b、c为常数）．
（Ⅰ）当b=1，c=﹣3时，求二次函数在﹣2≤x≤2上的最小值；
（Ⅱ）当c=3时，求二次函数在0≤x≤4上的最小值；
（Ⅲ）当c=4b2时，若在自变量x的值满足2b≤x≤2b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】看图填空：
已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠ADC=90°，∠EFC=90°（垂线的定义）
∴ =
∥
∴∠1=
∠2=
∵∠1=∠2（已知）
∴ =
∴AD平分∠BAC（角平分线定义）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）如图，抛物线
与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴l为
．
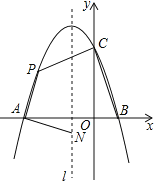
（1）求抛物线的解析式并写出其顶点坐标；
（2）若动点P在第二象限内的抛物线上，动点N在对称轴l上．
①当PA⊥NA，且PA=NA时，求此时点P的坐标；
②当四边形PABC的面积最大时，求四边形PABC面积的最大值及此时点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
