
【题目】(10分)如图,抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() .
.
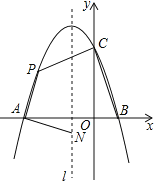
(1)求抛物线的解析式并写出其顶点坐标;
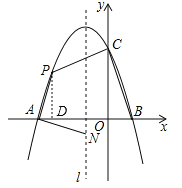
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
【答案】(1)![]() ,(﹣1,4);(2)①P(
,(﹣1,4);(2)①P(![]() ,2);②
,2);②![]() ,P(
,P(![]() ,
, ![]() ).
).
【解析】试题分析:(1)将B、C的坐标代入已知的抛物线的解析式,由对称轴为![]() 即可得到抛物线的解析式;
即可得到抛物线的解析式;
(2)①首先求得抛物线与x轴的交点坐标,然后根据已知条件得到PD=OA,从而得到方程求得x的值即可求得点P的坐标;
②![]() ,表示出来得到二次函数,求得最值即可.
,表示出来得到二次函数,求得最值即可.
试题解析:(1)∵抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() ,∴
,∴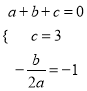 ,解得:
,解得: 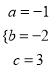 ,∴二次函数的解析式为
,∴二次函数的解析式为![]() =
=![]() ,∴顶点坐标为(﹣1,4);
,∴顶点坐标为(﹣1,4);
(2)令![]() ,解得
,解得![]() 或
或![]() ,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在
,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在![]() 上,∴设点P(x,
上,∴设点P(x, ![]() ),
),
①∵PA⊥NA,且PA=NA,∴△PAD≌△AND,∴OA=PD,即![]() ,解得x=
,解得x=![]() (舍去)或x=
(舍去)或x=![]() ,∴点P(
,∴点P(![]() ,2);
,2);
②设P(x,y),则![]() ,∵
,∵![]()
=![]() OBOC+
OBOC+![]() ADPD+
ADPD+![]() (PD+OC)OD=
(PD+OC)OD=![]() =
= ![]()
=![]() =
=![]() =
=![]() ,
,
∴当x=![]() 时,
时, ![]() =
=![]() ,当x=
,当x=![]() 时,
时, ![]() =
=![]() ,此时P(
,此时P(![]() ,
, ![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4 ![]() cm;④AC=8
cm;④AC=8 ![]() cm;⑤S菱形ABCD=80cm,正确的有( )
cm;⑤S菱形ABCD=80cm,正确的有( ) 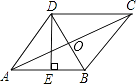
A.①②④⑤
B.①②③④
C.①③④⑤
D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,∠A+∠B =900.
⑴根据要求画图:
①过点C画直线 MN ∥AB
②过点C画AB的垂线,交AB于点D.
⑵请在⑴的基础上回答下列问题:
①已知∠B+∠DCB=900,则∠A与∠DCB 的大小关系为__________,理由是__________.
②图中线段_________的长度表示点 A 到直线CD的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com