
【题目】如图,△ABC 中,∠A+∠B =900.
⑴根据要求画图:
①过点C画直线 MN ∥AB
②过点C画AB的垂线,交AB于点D.
⑵请在⑴的基础上回答下列问题:
①已知∠B+∠DCB=900,则∠A与∠DCB 的大小关系为__________,理由是__________.
②图中线段_________的长度表示点 A 到直线CD的距离.

科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 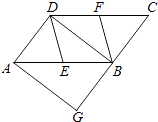
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( ).
A.所有等腰三角形都相似B.两边成比例的两个等腰三角形相似
C.有一个角相等的两个等腰三角形相似D.有一个角是100°的两个等腰三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某足球特色学校在商场购买甲、乙两种品牌的足球.已知乙种足球比甲种足球每只贵20元,该校分别花费2000元、1400元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球数量的2倍,求甲、乙两种足球的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2bx+c(b、c为常数).
(Ⅰ)当b=1,c=﹣3时,求二次函数在﹣2≤x≤2上的最小值;
(Ⅱ)当c=3时,求二次函数在0≤x≤4上的最小值;
(Ⅲ)当c=4b2时,若在自变量x的值满足2b≤x≤2b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
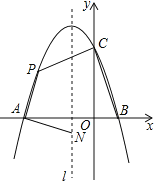
【题目】(10分)如图,抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.正方形的周长C随着边长x的变化而变化
C.水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t(min)的变化而变化
D.面积为20的三角形的一边a随着这边上的高h的变化而变化
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com