
 如图,直线y=kx+b与抛物线y=ax2相交于点A,B,与x轴相交于点C.
如图,直线y=kx+b与抛物线y=ax2相交于点A,B,与x轴相交于点C.分析 (1)将y=0代入y=kx+b,求出x的值,得出点C的横坐标,进而求解即可;
(2)将y=kx+b代入y=ax2,整理得ax2-kx-b=0,与根与系数的关系得出xA+xB=$\frac{k}{a}$,xA•xB=-$\frac{b}{a}$,那么$\frac{1}{{x}_{A}}$+$\frac{1}{{x}_{B}}$=$\frac{{x}_{A}+{x}_{B}}{{x}_{A}•{x}_{B}}$=$\frac{\frac{k}{a}}{-\frac{b}{a}}$=-$\frac{k}{b}$,又xC=-$\frac{b}{k}$,所以$\frac{1}{{x}_{C}}$=-$\frac{k}{b}$,从而证明$\frac{1}{{x}_{A}}$+$\frac{1}{{x}_{B}}$=$\frac{1}{{x}_{C}}$;
(3)根据a=b=$\frac{1}{2}$,∠ACO=30°得出直线解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{1}{2}$,抛物线解析式为y=$\frac{1}{2}$x2,再求出A、B两点的坐标,过A、B两点分别作x轴的垂线,垂足分别为D、E,根据S△AOB=S梯形ABED-S△AOD-S△BOE,计算即可求解.
解答 (1)解:∵y=kx+b与x轴相交于点C,
而当y=0时,kx+b=0,解得x=-$\frac{b}{k}$,
∴点C的坐标为(-$\frac{b}{k}$,0);
(2)证明:将y=kx+b代入y=ax2,
整理得ax2-kx-b=0,
∵直线y=kx+b与抛物线y=ax2相交于点A,B,
∴xA+xB=$\frac{k}{a}$,xA•xB=-$\frac{b}{a}$,
∴$\frac{1}{{x}_{A}}$+$\frac{1}{{x}_{B}}$=$\frac{{x}_{A}+{x}_{B}}{{x}_{A}•{x}_{B}}$=$\frac{\frac{k}{a}}{-\frac{b}{a}}$=-$\frac{k}{b}$,
∵xC=-$\frac{b}{k}$,
∴$\frac{1}{{x}_{C}}$=-$\frac{k}{b}$,
∴$\frac{1}{{x}_{A}}$+$\frac{1}{{x}_{B}}$=$\frac{1}{{x}_{C}}$;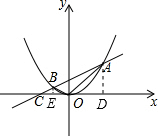 (3)解:∵a=b=$\frac{1}{2}$,∠ACO=30°,
(3)解:∵a=b=$\frac{1}{2}$,∠ACO=30°,
∴直线解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{1}{2}$,抛物线解析式为y=$\frac{1}{2}$x2,
将y=$\frac{\sqrt{3}}{3}$x+$\frac{1}{2}$代入y=$\frac{1}{2}$x2,
整理得$\frac{1}{2}$x2-$\frac{\sqrt{3}}{3}$x-$\frac{1}{2}$=0,
解得x1=$\sqrt{3}$,x2=-$\frac{\sqrt{3}}{3}$,
∴A($\sqrt{3}$,$\frac{3}{2}$),B(-$\frac{\sqrt{3}}{3}$,$\frac{1}{6}$).
如图,过A、B两点分别作x轴的垂线,垂足分别为D、E,
则S△AOB=S梯形ABED-S△AOD-S△BOE
=$\frac{1}{2}$(AD+BE)•DE-$\frac{1}{2}$AD•OD-$\frac{1}{2}$OE•BE
=$\frac{1}{2}$($\frac{3}{2}$+$\frac{1}{6}$)•($\sqrt{3}$+$\frac{\sqrt{3}}{3}$)-$\frac{1}{2}$×$\frac{3}{2}$×$\sqrt{3}$-$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$×$\frac{1}{6}$
=$\frac{10\sqrt{3}}{9}$-$\frac{3\sqrt{3}}{4}$-$\frac{\sqrt{3}}{36}$
=$\frac{\sqrt{3}}{3}$.
点评 本题是二次函数综合题,其中涉及到二次函数与一元二次方程的关系,一次函数图象上点的坐标特征,根与系数的关系,直线斜率的意义,两函数交点坐标的求法,三角形的面积等知识,综合性较强,难度适中.利用根与系数的关系是解决(2)的关键;理解直线斜率的意义得出直线解析式是解决(3)的关键.


科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴交于A,B两点,与y轴交于点C,顶点为点P,动点M,N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB,OC上向点B,C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴交于A,B两点,与y轴交于点C,顶点为点P,动点M,N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB,OC上向点B,C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 求解下面的不等式组,并将解集画在数轴上.
求解下面的不等式组,并将解集画在数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=(t-1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.
如图,二次函数y=(t-1)x2+(t+1)x+2(t≠1),x=0与x=3时的函数值相等,其图象与x轴交于A、B两点,与y轴正半轴交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图.在平面直角坐标系xOy中.点A的坐标为(-1,1),点B是x轴上的一动点.以AB为斜边作等腰直角△ABC,AM⊥x轴于M.当点C(x,y)在第一象限内时,下列图象中,可以表示y与x的函数关系的是( )
如图.在平面直角坐标系xOy中.点A的坐标为(-1,1),点B是x轴上的一动点.以AB为斜边作等腰直角△ABC,AM⊥x轴于M.当点C(x,y)在第一象限内时,下列图象中,可以表示y与x的函数关系的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
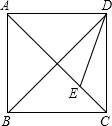 如图,在正方形ABCD中,DE是∠BDC的平分线,若CE的长是1,则正方形的边长是( )
如图,在正方形ABCD中,DE是∠BDC的平分线,若CE的长是1,则正方形的边长是( )| A. | 2 | B. | $\frac{\sqrt{2}}{2}$+1 | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com