
����Ŀ��ij���ܻ��س�������ͷ������������ԣ��䵥��Ϊ����������12Ԫ/�裬����������15Ԫ/�衣���ͬһ�ͻ������������Ե���������800�裬��ôÿ������ɽ���2Ԫ��ij�������۵��ܻ��زɹ�����400�衫900�裬�����������裬�����۵걾�����ڲɹ�����ͷ�����ǡ�û�ȥ12000Ԫ��Ȼ����������15Ԫ��������20Ԫ�ĵ���ʵ����������ɹ�����x�裬������y�裬ë����ΪWԪ��

��1����![]() ʱ��y��x��������ϵ��_______��W��x�ĺ�������ʽ��_________��
ʱ��y��x��������ϵ��_______��W��x�ĺ�������ʽ��_________��
��![]() ʱ��y��x��������ϵ��___________��W��x�ĺ�������ʽ��________��
ʱ��y��x��������ϵ��___________��W��x�ĺ�������ʽ��________��
��2���˻������۵�Ӧ��βɹ����������Բ���ʹ���ë�������
���𰸡���1����![]() ʱ��
ʱ��![]() ������
������![]() ����
����![]() ����
����![]() ʱ��
ʱ�� ![]() ������
������![]() ����
����![]() ����2���ɹ�����900�裬������200�裬ë�������Ϊ5500Ԫ
����2���ɹ�����900�裬������200�裬ë�������Ϊ5500Ԫ
��������
��1���������⣬��ֱ���г���ϵʽ��
��2���������⣬��������з����������ó��ɹ�����900�裬������200�裬ë�������Ϊ5500Ԫ.
��1���������⣬�ɵ�
��![]() ʱ��
ʱ��
![]() ������
������![]() ����
����
![]()
��![]() ��
��
��![]() ʱ��
ʱ��
![]() ������
������![]() ����
����
![]()
��![]() ��
��
��2����![]() ʱ��
ʱ��![]()
��![]() ��W����x���������С
��W����x���������С
�൱xȡ400ʱ��![]() ��W�����ֵ3600��
��W�����ֵ3600��
��![]() ʱ��
ʱ��![]()
��![]() ��W����x�����������
��W����x�����������
�൱xȡ900ʱ��![]() ��W�����ֵ5500��
��W�����ֵ5500��
�����������ɹ�����900�裬������200�裬ë�������Ϊ5500Ԫ


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪѧУ���������Ṻ��Ʒ����ij�ľ���Ʒ�깺������Ƭ��ÿһ������Ƭ�ļ۸���8Ԫ���ڽ���ʱ���֣�����ٶ���5�ţ��Ϳ������ܵ�����۵��Żݣ��ܼ۸�����8Ԫ��Ϊ���������Żݣ�����ʦ��ԭ�ƻ������5������Ƭ��
��1������ʦʵ�ʹ������������Ƭ��һ�����˶���Ǯ��
��2���ľߵ꿪չԪ���Żݻ���Ӽ�������һ���ڣ�ƾ����СƱ���ۼƹ��ﳬ��500Ԫ���������ֿ������ܰ��۵��Żݣ�����ʦ����һ�룬��ΪѧУ������һ�������ıʼDZ��������˰����Żݣ�����������һ����ʡ��36Ԫ������ʦ����ʼDZ�ʵ�ʻ��˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���û����ڳ�һ��������ͼ�����ڢٸ�ͼ������ 4 �����ڢڸ�ͼ������ 12 �����ڢ۸�ͼ������ 24 �����������ַ�ʽ����ȥ���ڳ��ڢ�ͼ���û����ĸ����ǣ� ��

A. 84 B. 81 C. 78 D. 76
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
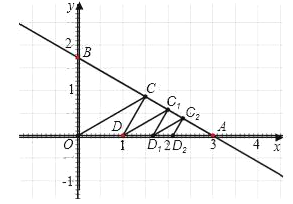
����Ŀ����ͼ����ƽ��ֱ������ϵ����ֱ��![]() ��x����A������y����B������C���߶�AB���е�������OC��Ȼ��ֱ��OC�Ƶ�C��ʱ����ת30����x���ڵ�D���ٹ�D����ֱ��DC1��OC����AB���C1��Ȼ���C1�������ֱ��D1C1��DC����x���ڵ�D1���������ظ����ϲ���������OCD�����ΪS1����DC1D1�����ΪS2���������������������������ֱ���S3��S4������ôS1=_____����S=S1+S2+S3+��+Sn����n����ʱ��S��ֵ���ӽ���_____��
��x����A������y����B������C���߶�AB���е�������OC��Ȼ��ֱ��OC�Ƶ�C��ʱ����ת30����x���ڵ�D���ٹ�D����ֱ��DC1��OC����AB���C1��Ȼ���C1�������ֱ��D1C1��DC����x���ڵ�D1���������ظ����ϲ���������OCD�����ΪS1����DC1D1�����ΪS2���������������������������ֱ���S3��S4������ôS1=_____����S=S1+S2+S3+��+Sn����n����ʱ��S��ֵ���ӽ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
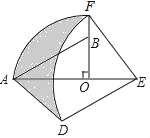
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=3��OB=2����Rt��AOB�Ƶ�O˳ʱ����ת90�����Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90������߶�ED���ֱ���O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺��y��z��2+��x��y��2+��z��x��2=��y+z��2x��2+��z+x��2y��2+��x+y��2z��2��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬����
��һ�㣬����![]() ������
������![]() ��ʹ
��ʹ![]() ����һֱ�����ǰ��ֱ�Ƕ�����ڵ�
����һֱ�����ǰ��ֱ�Ƕ�����ڵ�![]() ����
����![]() ����һ��
����һ��![]() ������
������![]() �ϣ���һ��
�ϣ���һ��![]() ��ֱ��
��ֱ��![]() ���·���
���·���

��1����ͼ1�е����ǰ��Ƶ�![]() ��ʱ����ת��ͼ2��ʹһ��
��ʱ����ת��ͼ2��ʹһ��![]() ��
��![]() ���ڲ�����ǡ��ƽ��
���ڲ�����ǡ��ƽ��![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ1�е����ǰ��Ƶ�![]() ��ÿ��5���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���
��ÿ��5���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���![]() ��ʱ��ֱ��
��ʱ��ֱ��![]() ǡ��ƽ�����
ǡ��ƽ�����![]() ����
����![]() ��ֵ��
��ֵ��
��ͼ1�е����ǰ��Ƶ�![]() ��ʱ����ת��ͼ3��ʹһ��
��ʱ����ת��ͼ3��ʹһ��![]() ��
��![]() ���ڲ�����̽��
���ڲ�����̽��![]() ��ֵ��/span>
��ֵ��/span>
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ����ֱ������ABCD�У���BAD=90�㣬E��ֱ��AB��һ�㣬��E��ֱ��l��BC����ֱ��CD�ڵ�F����ֱ��l����ƽ�ƣ���ƽ�ƾ���BEΪt��t��0����ֱ������ABCD��ֱ��lɨ���������ͼ����Ӱ���֣�ΪS��S����t�ĺ���ͼ����ͼ����ʾ��OMΪ�߶Σ�MNΪ�����ߵ�һ���֣�NQΪ���ߣ�N�������Ϊ4��
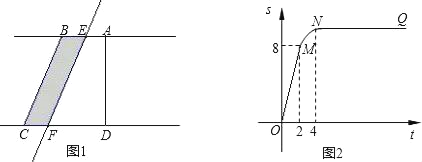
��Ϣ��ȡ
��1�������ϵij�AB=�� ����
��2��ֱ������ABCD�����=�� ����
ͼ������
��3��д��ͼ��������NQ��ʾ��ʵ�����壻
��4����2��t��4ʱ����S����t�ĺ�����ϵʽ��
������
��5����tΪ��ֵʱ��ֱ��l��ֱ������ABCD�ֳɵ����������֮��Ϊ1��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
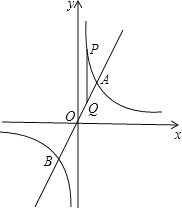
����Ŀ����ͼ����ֱ֪��y=kx(k>0)��˫����![]() ����A��B���㣬�ҵ�A��������Ϊ4,��һ����˫��������һ��
����A��B���㣬�ҵ�A��������Ϊ4,��һ����˫��������һ��![]() ,����P��PQ//y�ύֱ��AB�ڵ�Q��
,����P��PQ//y�ύֱ��AB�ڵ�Q��
��1��ֱ��д��k��ֵ����B�����꣺
��2�����߶�PQ�ij���
��3�������ֱ��y=kx����һ��M,��������BPM���������12,���M�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com