
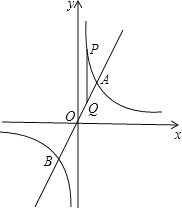
【题目】如图,已知直线y=kx(k>0)与双曲线![]() 交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点
交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点![]() ,过点P作PQ//y轴交直线AB于点Q.
,过点P作PQ//y轴交直线AB于点Q.
(1)直接写出k的值及点B的坐标:
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
【答案】(1)![]() ;(2)6;(3)点M的坐标
;(2)6;(3)点M的坐标![]() 或
或![]()
【解析】
(1)先求得A点坐标,再代入直线解析式可求得k的值,根据对称性可求得B点坐标;
(2)由反比例函数解析式可求得P点坐标,由直线解析式可求得Q点坐标,可求得PQ的长;
(3)可设M坐标为(m,2m),分点M在线段BQ的延长线上和线段QB的延长线上两种情况,分别表示出△BPM的面积,可求得m的值,可求得M的坐标.
解:(1)∵A在双曲线![]() 上,且A的纵坐标为4,
上,且A的纵坐标为4,
∴A坐标为(2,4),
代入直线y=kx,可得4=2k,解得k=2,
又A、B关于原点对称,
∴点B的坐标为(-2,-4).
(2)∵点P(1,a)在双曲线上,
∴代入![]() ,可得点P的坐标为(1,8).
,可得点P的坐标为(1,8).
∵PQ∥y轴,且点Q在直线AB上,
∴可设点Q的坐标为(1,b).
代入y=2x,得点Q的坐标为(1,2).
∴PQ=6.
(3)设点M的坐标为(m,2m).
![]()
①当点M在BQ的延长线上时,S△BPM=S△BPQ+S△MPQ,![]()
点M的坐标为(2,4).
②当点M在QB的延长线上时,S△BPM=S△MPQ-S△BPQ,![]()
点M的坐标为(-6,-12).
综上所述:点M的坐标为(2,4),(-6,-12).


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】某花卉基地出售文竹和发财树两种盆栽,其单价为:文竹盆栽12元/盆,发财树盆栽15元/盆。如果同一客户所购文竹盆栽的数量大于800盆,那么每盆文竹可降价2元.某花卉销售店向花卉基地采购文竹400盆~900盆,发财树若干盆,此销售店本次用于采购文竹和发财树恰好花去12000元.然后再以文竹15元,发财树20元的单价实卖出.若设采购文竹x盆,发财树y盆,毛利润为W元.

(1)当![]() 时,y与x的数量关系是_______,W与x的函数解析式是_________;
时,y与x的数量关系是_______,W与x的函数解析式是_________;
当![]() 时,y与x的数量关系是___________,W与x的函数解析式是________;
时,y与x的数量关系是___________,W与x的函数解析式是________;
(2)此花卉销售店应如何采购这两种盆栽才能使获得毛利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
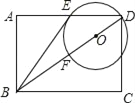
【题目】已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.
(1)判断直线BE与⊙O的位置关系,并证明你的结论;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
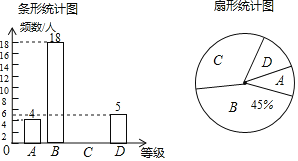
【题目】某学校为了解今年八年级学生足球运球的掌握情况,随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行如图不完整的统计图根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图、扇形统计图;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
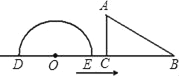
【题目】如图,已知半圆O的直径DE=12cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
(1)当t为何值时,△ABC的一边所在直线与半圆O所在的圆相切?
(2)当△ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成![]() ,
,![]() ,
,![]() ,
,![]() 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).
![]() 组:
组:![]() 组:
组:![]() 组:
组:![]() 组:
组:![]()

请根据上述信息解答下列问题:
(1)![]() 组的人数是 ;
组的人数是 ;
(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
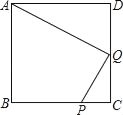
【题目】如图,P是正方形ABCD边BC上的一点,且BP=3PC,Q是CD中点.
(1)求证:△ADQ∽△QCP.
(2)试问:AQ与PQ有什么关系(位置与数量)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月19日为第29个“全国助残日”我市某中学组织了献爱心捐款活动,该校数学课外活动小组对本次捐款活动做了一次抽样调查,并绘制了如下不完整的频数分布表和频数分布直方图(每组含前一个边界,不含后一个边界).
捐款额(元) | 频数 | 百分比 |
| 3 | 7.5% |
| 7 | 17.5% |
| a | b |
| 10 | 25% |
| 6 | 15% |
总计 | 100% |
(1)填空:![]() ________,
________,![]() ________.
________.
(2)补全频数分布直方图.
(3)该校有2000名学生估计这次活动中爱心捐款额在![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
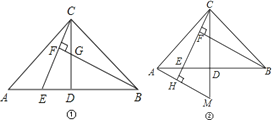
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点 H,交CD的延长线于点M(如图②),
求证:CM=BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com