
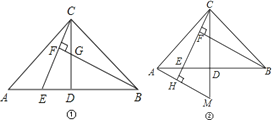
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点 H,交CD的延长线于点M(如图②),
求证:CM=BE.
【答案】(1)见详解;(2)见详解.
【解析】
(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)证明:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,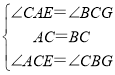
∴△AEC≌△CGB(ASA),
∴AE=CG,
(2)
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,
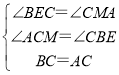 ∴△BCE≌△CAM(AAS),
∴△BCE≌△CAM(AAS),
∴BE=CM.


科目:初中数学 来源: 题型:
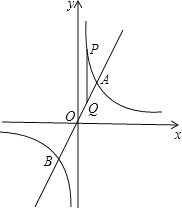
【题目】如图,已知直线y=kx(k>0)与双曲线![]() 交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点
交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点![]() ,过点P作PQ//y轴交直线AB于点Q.
,过点P作PQ//y轴交直线AB于点Q.
(1)直接写出k的值及点B的坐标:
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从![]() 、
、![]() 出发,沿直线轨道同时到达
出发,沿直线轨道同时到达![]() 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与
处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与![]() 处的距离
处的距离![]() 、
、![]() (米)与时间
(米)与时间![]() (分钟)的函数关系如图所示,则下列结论中:①
(分钟)的函数关系如图所示,则下列结论中:①![]() 的距离为120米;②乙的速度为60米/分;③
的距离为120米;②乙的速度为60米/分;③![]() 的值为
的值为![]() ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的
;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的![]() 的取值范围是
的取值范围是![]() ,其中正确的有( )个
,其中正确的有( )个
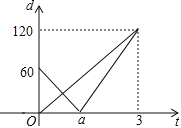
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果一个点的纵坐标等于横坐标的2倍,那么这个点叫做倍点.例如:点(1,2)是倍点。
(1)已知第一象限内的点A到x轴的距离是1,若点A是倍点,则点A的坐标为________
(2)求反比例函数![]() 图像上的所有倍点;
图像上的所有倍点;
(3)请分析一次函数![]() (
(![]() 为常数)图像上倍点的情况.
为常数)图像上倍点的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚和小强从![]() 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达
两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达![]() 地.
地.
(1)两人的行进速度分别是多少?
(2)相遇后经过多少时间小强到达![]() 地?
地?
(3)![]() 两地相距多少千米?
两地相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,求线段
的中点,求线段![]() 的长度;
的长度;
![]()
(2)若点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,请直接写出线段
的中点,请直接写出线段![]() 的长度;(结果用含
的长度;(结果用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(3)在(2)中,把点![]() 是线段
是线段![]() 上任意一点改为:点
上任意一点改为:点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
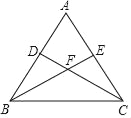
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com