
【题目】小刚和小强从![]() 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达
两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达![]() 地.
地.
(1)两人的行进速度分别是多少?
(2)相遇后经过多少时间小强到达![]() 地?
地?
(3)![]() 两地相距多少千米?
两地相距多少千米?
【答案】(1)小强的速度为4千米/小时,小刚的速度为16千米/小时;(2)在经过8小时,小强到达目的地;(3)AB两地相距40千米.
【解析】
(1)根据已知条件,可设小强的速度为x千米/小时,则小刚的速度为(x+12)千米/小时,再根据“相遇后0.5小时小刚到达![]() 地”列出方程求解即可;
地”列出方程求解即可;
(2)设在经过y小时,小强到达目的地,根据“相遇后小强的行程等于相遇前小刚的行程”列出方程求解;
(3)根据AB之间的距离等于相遇时两人的路程之和计算即可.
解:(1)设小强的速度为x千米/小时,则小刚的速度为(x+12)千米/小时.
根据题意得:2x=0.5(x+12).
解得:x=4.
x+12=4+12=16.
答:小强的速度为4千米/小时,小刚的速度为16千米/小时.
(2)设在经过y小时,小强到达目的地.
根据题意得:4y=2×16.
解得:y=8.
答:在经过8小时,小强到达目的地.
(3)2×4+2×16=40(千米).
答:AB两地相距40千米.


科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成![]() ,
,![]() ,
,![]() ,
,![]() 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).
![]() 组:
组:![]() 组:
组:![]() 组:
组:![]() 组:
组:![]()

请根据上述信息解答下列问题:
(1)![]() 组的人数是 ;
组的人数是 ;
(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在生活中经常使用的数是十进制数,如![]() ,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字
,表示十进制的数要用到10个数码(也叫数字):0,1,2,3,4,5,6,7,8,9.计算机中常用的十六进制是逢16进1的计数制,采用数字![]() 和字母
和字母![]() 共16个计数符号,这些符号与十进制的对应关系如下表
共16个计数符号,这些符号与十进制的对应关系如下表
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如:十六进制数![]() ,即十六进制数71B相当于十进制数1819.那么十六进制数2E8相当于十进制数( )
,即十六进制数71B相当于十进制数1819.那么十六进制数2E8相当于十进制数( )
A.744B.736C.536D.512
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
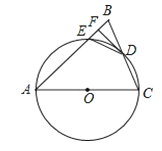
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点 H,交CD的延长线于点M(如图②),
求证:CM=BE.
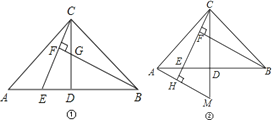
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D的坐标分别为(-2,2),(一2,1),(3,1),(3,2),线段AD、AB、BC组成的图形记作G,点P沿D-A-B-C移动,设点P移动的距离为a,直线l:y=-x+b过点P,且在点P移动过程中,直线l随点P移动而移动,若直线l过点C,求
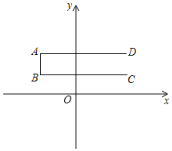
(1)直线l的解析式;
(2)求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,将一直角三角板如图摆放(
,将一直角三角板如图摆放(![]() ).
).
(1)若![]() ,求
,求![]() 的大小.
的大小.
(2)将图①中的三角板绕点![]() 旋转一定的角度得图②,使边
旋转一定的角度得图②,使边![]() 恰好平分
恰好平分![]() ,问:
,问:![]() 是否平分
是否平分![]() ?请说明理由.
?请说明理由.
(3)将图①中的三角板绕点![]() 旋转一定的角度得图③,使边
旋转一定的角度得图③,使边![]() 在
在![]() 的内部,如果
的内部,如果![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系?请说明理由.
之间存在怎样的数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题研究
(1)阅读下面材料:
如图所示,点A、B在数轴上分别表示有理数a,b,A、B两点之间的距离表示为![]() .当A、B两点中有一点在原点时,不妨设点A在原点,如图甲所示,
.当A、B两点中有一点在原点时,不妨设点A在原点,如图甲所示,![]() ;当A、B两点都不在原点时:
;当A、B两点都不在原点时:
①如图乙所示,点A、B都在原点的右边,![]()
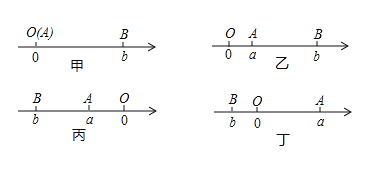
②如图丙所示,点A、B都在原点的左边,![]()
③如图丁所示,点A、B在原点的两边,![]()
综上,数轴上A、B两点之间的距离为![]() =______________________.
=______________________.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是_______
②数轴上表示-2和-5的两点之间的距离是_______
③数轴上表示1和-3的两点之间的距离是_______
④数轴上表示x和-1的两点之间的距离是_______
⑤如果![]() =2,那么x的值为______________
=2,那么x的值为______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
(应用):
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
(拓展):
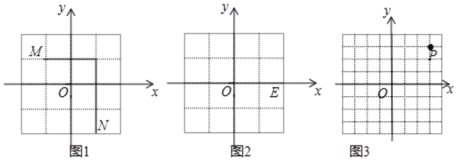
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)已知E(2,0),若F(﹣1,﹣2),求d(E,F);
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,求t的值;
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com