
【题目】课题研究
(1)阅读下面材料:
如图所示,点A、B在数轴上分别表示有理数a,b,A、B两点之间的距离表示为![]() .当A、B两点中有一点在原点时,不妨设点A在原点,如图甲所示,
.当A、B两点中有一点在原点时,不妨设点A在原点,如图甲所示,![]() ;当A、B两点都不在原点时:
;当A、B两点都不在原点时:
①如图乙所示,点A、B都在原点的右边,![]()
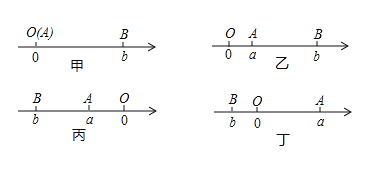
②如图丙所示,点A、B都在原点的左边,![]()
③如图丁所示,点A、B在原点的两边,![]()
综上,数轴上A、B两点之间的距离为![]() =______________________.
=______________________.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是_______
②数轴上表示-2和-5的两点之间的距离是_______
③数轴上表示1和-3的两点之间的距离是_______
④数轴上表示x和-1的两点之间的距离是_______
⑤如果![]() =2,那么x的值为______________
=2,那么x的值为______________
科目:初中数学 来源: 题型:
【题目】 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
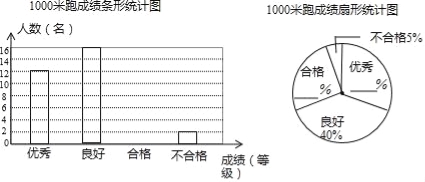
(1)根据给出的信息,补全两幅统计图;
(2)该校九年级有600名男生,请估计成绩未达到良好有多少名?
(3)某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚和小强从![]() 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达
两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达![]() 地.
地.
(1)两人的行进速度分别是多少?
(2)相遇后经过多少时间小强到达![]() 地?
地?
(3)![]() 两地相距多少千米?
两地相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,求线段
的中点,求线段![]() 的长度;
的长度;
![]()
(2)若点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,请直接写出线段
的中点,请直接写出线段![]() 的长度;(结果用含
的长度;(结果用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(3)在(2)中,把点![]() 是线段
是线段![]() 上任意一点改为:点
上任意一点改为:点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
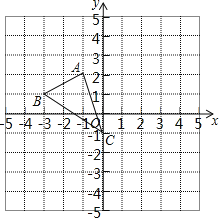
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.
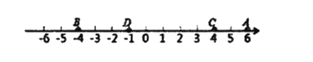
问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com