
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,将一直角三角板如图摆放(
,将一直角三角板如图摆放(![]() ).
).
(1)若![]() ,求
,求![]() 的大小.
的大小.
(2)将图①中的三角板绕点![]() 旋转一定的角度得图②,使边
旋转一定的角度得图②,使边![]() 恰好平分
恰好平分![]() ,问:
,问:![]() 是否平分
是否平分![]() ?请说明理由.
?请说明理由.
(3)将图①中的三角板绕点![]() 旋转一定的角度得图③,使边
旋转一定的角度得图③,使边![]() 在
在![]() 的内部,如果
的内部,如果![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系?请说明理由.
之间存在怎样的数量关系?请说明理由.

【答案】(1)125°;(2)ON平分∠AOC,理由详见解析;(3)∠BOM=∠NOC+40°,理由详见解析
【解析】
(1)根据∠MOC=∠MON+∠BOC计算即可;
(2)由角平分线定义得到角相等的等量关系,再根据等角的余角相等即可得出结论;
(3)根据题干已知条件将一个角的度数转换为两个角的度数之和,列出等式即可得出结论.
解: (1) ∵∠MON=90° , ∠BOC=35°,
∴∠MOC=∠MON+∠BOC= 90°+35°=125°.
(2)ON平分∠AOC.
理由如下:
∵∠MON=90°,
∴∠BOM+∠AON=90°,∠MOC+∠NOC=90°.
又∵OM平分∠BOC,∴∠BOM=∠MOC.
∴∠AON=∠NOC.
∴ON平分∠AOC.
(3)∠BOM=∠NOC+40°.
理由如下:
∵∠CON+∠NOB=50°,∴∠NOB=50°-∠NOC.
∵∠BOM+∠NOB=90°,
∴∠BOM=90°-∠NOB=90°-(50°-∠NOC)=∠NOC+40°.


科目:初中数学 来源: 题型:
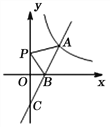
【题目】如图,一次函数y=2x+b的图象与反比例函数![]() (x>0)的图象交于点A(m,2),与坐标轴分别交于B和C(0,-2)两点.
(x>0)的图象交于点A(m,2),与坐标轴分别交于B和C(0,-2)两点.
(1)求反比例函数的表达式;
(2)若P是y轴上一动点,当PA+PB的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚和小强从![]() 两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达
两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行.出发后两小时两人相遇,相遇时小刚比小强多行进24千米.相遇后0.5小时小刚到达![]() 地.
地.
(1)两人的行进速度分别是多少?
(2)相遇后经过多少时间小强到达![]() 地?
地?
(3)![]() 两地相距多少千米?
两地相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,求线段
的中点,求线段![]() 的长度;
的长度;
![]()
(2)若点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,请直接写出线段
的中点,请直接写出线段![]() 的长度;(结果用含
的长度;(结果用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(3)在(2)中,把点![]() 是线段
是线段![]() 上任意一点改为:点
上任意一点改为:点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com