
【题目】如图,折叠长方形的一边![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处,已知
处,已知![]() ,
,![]() .
.
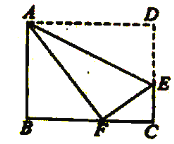
(1)求![]() 的长;
的长;
(2)求![]() 的长.
的长.
【答案】(1)EC的长为3cm;(2)AE=![]() .
.
【解析】
(1)根据折叠可得△ADE≌△AFE,设EF=ED =x则EC=8-x,在直角△ABF中,由勾股定理求出BF=6,得到FC =4,在直角△EFC中,由勾股定理可得x2=42+(8-x)2即可求出x,故可求解;
(2)利用AE=![]() 即可求解.
即可求解.
(1)∵四边形ABCD为长方形,
∴AD=BC=10,DC=AB=8;
由题意得:△ADE≌△AFE,
∴AF=AD=10,EF=ED(设为x),
则EC=8-x;
在直角△ABF中,
由勾股定理得:
BF=![]()
∴FC=10-6=4;
在直角△EFC中,
由勾股定理得:
x2=42+(8-x)2,
解得:x=5,8-x=3;
∴EC的长为3(cm).
(2)由勾股定理得:
AE=![]()


科目:初中数学 来源: 题型:
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,将一直角三角板如图摆放(
,将一直角三角板如图摆放(![]() ).
).
(1)若![]() ,求
,求![]() 的大小.
的大小.
(2)将图①中的三角板绕点![]() 旋转一定的角度得图②,使边
旋转一定的角度得图②,使边![]() 恰好平分
恰好平分![]() ,问:
,问:![]() 是否平分
是否平分![]() ?请说明理由.
?请说明理由.
(3)将图①中的三角板绕点![]() 旋转一定的角度得图③,使边
旋转一定的角度得图③,使边![]() 在
在![]() 的内部,如果
的内部,如果![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系?请说明理由.
之间存在怎样的数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在直角坐标系中,
在直角坐标系中,![]() 各点的坐标分别为
各点的坐标分别为![]() ,
,![]() ,
,![]() ;
;

(1)若把![]() 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到![]() ,写出
,写出![]() 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形.
(2)求出三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
(应用):
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
(拓展):
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)已知E(2,0),若F(﹣1,﹣2),求d(E,F);
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,求t的值;
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).
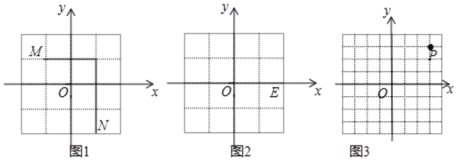
查看答案和解析>>
科目:初中数学 来源: 题型:
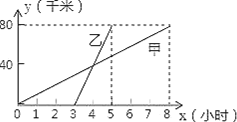
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)甲先出发______小时后,乙才出发;大约在甲出发______小时后,两人相遇,这时他们离A地_______千米.
(2)两人的行驶速度分别是多少?
(3)分别写出表示甲、乙的路程y(千米)与时间x(小时)之间的函数表达式(不要求写出自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第10个图形中花盆的个数为( )

A. 110B. 120C. 132D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
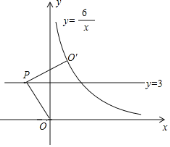
【题目】如图,点P是直线y=3上的动点,连接PO并将PO绕P点旋转90°到PO′,当点O′刚好落在双曲线![]() (x>0)上时,点P的横坐标所有可能值为_____.
(x>0)上时,点P的横坐标所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
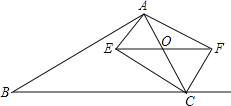
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com