
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯвЛЕуЃЌЙ§Еу
ЩЯвЛЕуЃЌЙ§Еу![]() зїЩфЯп
зїЩфЯп![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌНЋвЛжБНЧШ§НЧАхЕФжБНЧЖЅЕуЗХдкЕу
ЃЌНЋвЛжБНЧШ§НЧАхЕФжБНЧЖЅЕуЗХдкЕу![]() ДІЃЈ
ДІЃЈ![]() ЃЉЃЌвЛБп
ЃЉЃЌвЛБп![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌСэвЛБп
ЩЯЃЌСэвЛБп![]() дкжБЯп
дкжБЯп![]() ЕФЯТЗНЃЎ
ЕФЯТЗНЃЎ

ЃЈ1ЃЉНЋЭМ1жаЕФШ§НЧАхШЦЕу![]() ФцЪБеыа§зЊжСЭМ2ЃЌЪЙвЛБп
ФцЪБеыа§зЊжСЭМ2ЃЌЪЙвЛБп![]() дк
дк![]() ЕФФкВПЃЌЧвЧЁКУЦНЗж
ЕФФкВПЃЌЧвЧЁКУЦНЗж![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉНЋЭМ1жаЕФШ§НЧАхШЦЕу![]() вдУПУы5ЕФЫйЖШбиФцЪБеыЗНЯђа§зЊвЛжмЃЌдка§зЊЕФЙ§ГЬжаЃЌЕк
вдУПУы5ЕФЫйЖШбиФцЪБеыЗНЯђа§зЊвЛжмЃЌдка§зЊЕФЙ§ГЬжаЃЌЕк![]() УыЪБЃЌжБЯп
УыЪБЃЌжБЯп![]() ЧЁКУЦНЗжШёНЧ
ЧЁКУЦНЗжШёНЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
НЋЭМ1жаЕФШ§НЧАхШЦЕу![]() ФцЪБеыа§зЊжСЭМ3ЃЌЪЙвЛБп
ФцЪБеыа§зЊжСЭМ3ЃЌЪЙвЛБп![]() дк
дк![]() ЕФФкВПЃЌЧыЬНОП
ЕФФкВПЃЌЧыЬНОП![]() ЕФжЕЃЎ/span>
ЕФжЕЃЎ/span>
ЁОД№АИЁПЃЈ1ЃЉ35ЁуЃЛЃЈ2ЃЉ11Лђ47ЃЛЃЈ3ЃЉЁЯAOM-ЁЯNOC=20ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнНЧЦНЗжЯпЕФЖЈвхЭЈЙ§МЦЫуМДПЩЧѓЕУЁЯBONЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЕБONЕФЗДЯђбгГЄЯпЦНЗжЁЯAOCЪБЛђЕБЩфЯпONЦНЗжЁЯAOCЪБетСНжжЧщПіЗжБ№ЬжТлЃЌИљОнНЧЦНЗжЯпЕФЖЈвхвдМАНЧЕФЙиЯЕНјааМЦЫуМДПЩЃЛ
ЃЈ3ЃЉИљОнЁЯMON=90ЁуЃЌЁЯAOC=70ЁуЃЌЗжБ№ЧѓЕУЁЯAOM=90Ёу-ЁЯAONЃЌЁЯNOC=70Ёу-ЁЯAONЃЌдйИљОнЁЯAOM-ЁЯNOC=ЃЈ90Ёу-ЁЯAONЃЉ-ЃЈ70Ёу-ЁЯAONЃЉНјааМЦЫуЃЌМДПЩЕУГіЁЯAOMгыЁЯNOCЕФЪ§СПЙиЯЕЃЎ
НтЃКЃЈ1ЃЉШчЭМ2жаЃЌ
ЁпOMЦНЗжЁЯBOCЃЌ
ЁрЁЯMOC=ЁЯMOBЃЌ
гжЁпЁЯBOC=110ЁуЃЌ
ЁрЁЯMOB=55ЁуЃЌ
ЁпЁЯMON=90ЁуЃЌ
ЁрЁЯBON=ЁЯMON-ЁЯMOB=35ЁуЃЛ
ЃЈ2ЃЉЃЈ2ЃЉЗжСНжжЧщПіЃК
ЂйШчЭМ2ЃЌЁпЁЯBOC=110Ёу
ЁрЁЯAOC=70ЁуЃЌ
ЕБЕБONЕФЗДЯђбгГЄЯпЦНЗжЁЯAOCЪБЃЌЁЯAOD=ЁЯCOD=35ЁуЃЌ
ЁрЁЯBON=35ЁуЃЌЁЯBOM=55ЁуЃЌ
МДФцЪБеыа§зЊЕФНЧЖШЮЊ55ЁуЃЌ
гЩЬтвтЕУЃЌ5t=55Ёу
НтЕУt=11ЃЛ
ЂкШчЭМ3ЃЌЕБЩфЯпONЦНЗжЁЯAOCЪБЃЌЁЯNOA=35ЁуЃЌ
ЁрЁЯAOM=55ЁуЃЌ
МДФцЪБеыа§зЊЕФНЧЖШЮЊЃК180Ёу+55Ёу=235ЁуЃЌ
гЩЬтвтЕУЃЌ5t=235ЁуЃЌ
НтЕУt=47ЃЌ
злЩЯЫљЪіЃЌt=11sЛђ47sЪБЃЌжБЯпONЧЁКУЦНЗжШёНЧЁЯAOCЃЛ
ЙЪД№АИЮЊЃК11Лђ47ЃЛ
ЃЈ3ЃЉЁЯAOM-ЁЯNOC=20ЁуЃЎ
РэгЩЃКЁпЁЯMON=90ЁуЃЌЁЯAOC=70ЁуЃЌ
ЁрЁЯAOM=90Ёу-ЁЯAONЃЌЁЯNOC=70Ёу-ЁЯAONЃЌ
ЁрЁЯAOM-ЁЯNOC=ЃЈ90Ёу-ЁЯAONЃЉ-ЃЈ70Ёу-ЁЯAONЃЉ=20ЁуЃЌ
ЁрЁЯAOMгыЁЯNOCЕФЪ§СПЙиЯЕЮЊЃКЁЯAOM-ЁЯNOC=20ЁуЃЎ


 гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
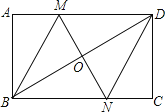
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЖдНЧЯпBDЕФДЙжБЦНЗжЯпMNгыADЯрНЛгкЕуMЃЌгыBDЯрНЛгкЕуOЃЌгыBCЯрНЛгкЕуNЃЌСЌНгBMЁЂDNЃЎ
![]() ЧѓжЄЃКЫФБпаЮBMDNЪЧСтаЮЃЛ
ЧѓжЄЃКЫФБпаЮBMDNЪЧСтаЮЃЛ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌЧѓСтаЮBMDNЕФУцЛ§КЭЖдНЧЯпMNЕФГЄЃЎ
ЃЌЧѓСтаЮBMDNЕФУцЛ§КЭЖдНЧЯпMNЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
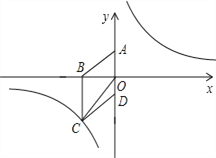
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЫФБпаЮABCDЮЊСтаЮЃЌЧв![]() ЃЈ0ЃЌ3ЃЉЁЂ
ЃЈ0ЃЌ3ЃЉЁЂ![]() ЃЈЉ4ЃЌ0ЃЉЃЎ
ЃЈЉ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓОЙ§Еу![]() ЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩш![]() ЪЧЃЈ1ЃЉжаЫљЧѓКЏЪ§ЭМЯѓЩЯвЛЕуЃЌвд
ЪЧЃЈ1ЃЉжаЫљЧѓКЏЪ§ЭМЯѓЩЯвЛЕуЃЌвд![]() ЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыЁїCODЕФУцЛ§ЯрЕШЃЎЧѓЕуPЕФзјБъЃЎ
ЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыЁїCODЕФУцЛ§ЯрЕШЃЎЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЛЈЛмЛљЕиГіЪлЮФжёКЭЗЂВЦЪїСНжжХшддЃЌЦфЕЅМлЮЊЃКЮФжёХшдд12дЊ/ХшЃЌЗЂВЦЪїХшдд15дЊ/ХшЁЃШчЙћЭЌвЛПЭЛЇЫљЙКЮФжёХшддЕФЪ§СПДѓгк800ХшЃЌФЧУДУПХшЮФжёПЩНЕМл2дЊЃЎФГЛЈЛмЯњЪлЕъЯђЛЈЛмЛљЕиВЩЙКЮФжё400ХшЁЋ900ХшЃЌЗЂВЦЪїШєИЩХшЃЌДЫЯњЪлЕъБОДЮгУгкВЩЙКЮФжёКЭЗЂВЦЪїЧЁКУЛЈШЅ12000дЊЃЎШЛКѓдйвдЮФжё15дЊЃЌЗЂВЦЪї20дЊЕФЕЅМлЪЕТєГіЃЎШєЩшВЩЙКЮФжёxХшЃЌЗЂВЦЪїyХшЃЌУЋРћШѓЮЊWдЊЃЎ

ЃЈ1ЃЉЕБ![]() ЪБЃЌyгыxЕФЪ§СПЙиЯЕЪЧ_______ЃЌWгыxЕФКЏЪ§НтЮіЪНЪЧ_________ЃЛ
ЪБЃЌyгыxЕФЪ§СПЙиЯЕЪЧ_______ЃЌWгыxЕФКЏЪ§НтЮіЪНЪЧ_________ЃЛ
ЕБ![]() ЪБЃЌyгыxЕФЪ§СПЙиЯЕЪЧ___________ЃЌWгыxЕФКЏЪ§НтЮіЪНЪЧ________ЃЛ
ЪБЃЌyгыxЕФЪ§СПЙиЯЕЪЧ___________ЃЌWгыxЕФКЏЪ§НтЮіЪНЪЧ________ЃЛ
ЃЈ2ЃЉДЫЛЈЛмЯњЪлЕъгІШчКЮВЩЙКетСНжжХшддВХФмЪЙЛёЕУУЋРћШѓзюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛжЛТьвЯДгдЕуOГіЗЂЃЌАДЯђЩЯЁЂЯђгвЁЂЯђЯТЁЂЯђгвЕФЗНЯђвРДЮВЛЖЯЕивЦЖЏЃЌУПДЮвЦЖЏ1ИіЕЅЮЛЃЎЦфаазпТЗЯпШчЭМЫљЪОЃЎ
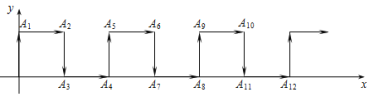
(1)ЬюаДЯТСаИїЕуЕФзјБъЃКA4(_____ЃЌ_____)ЃЌA8(_____ЃЌ_____)ЃЌA10(______ЃЌ____)ЃЌA12(_____ЃЌ____)ЃЛ
(2)аДГіЕуA4nЕФзјБъ(nЪЧе§ећЪ§)ЃЛ (3)жИГіТьвЯДгЕуA2017ЕНЕуA2018ЕФвЦЖЏЗНЯђЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
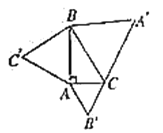
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЖШ.вд
ЖШ.вд![]() ЕФШ§БпЮЊБпЗжБ№ЯђЭтзїЕШБпШ§НЧаЮ
ЕФШ§БпЮЊБпЗжБ№ЯђЭтзїЕШБпШ§НЧаЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЗжБ№ЪЧ8КЭ3ЃЌдђ
ЕФУцЛ§ЗжБ№ЪЧ8КЭ3ЃЌдђ![]() ЕФУцЛ§ЪЧЃЈ ЃЉ
ЕФУцЛ§ЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊA=2a2+3abЉ2aЉ1ЃЌB=Љa2+![]() ab+
ab+![]() ЃЎ
ЃЎ
ЃЈ1ЃЉa=Љ1ЃЌb=Љ2ЪБЃЌЧѓ4AЉЃЈ3AЉ2BЃЉЕФжЕЃЛ
ЃЈ2ЃЉШєЃЈ1ЃЉжаЪНзгЕФжЕгыaЕФШЁжЕЮоЙиЃЌЧѓbЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
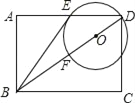
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкОиаЮABCDжаЃЌЕуOдкЖдНЧЯпBDЩЯЃЌвдODЕФГЄЮЊАыОЖЕФЁбOгыADЃЌBDЗжБ№НЛгкЕуEЁЂЕуFЃЌЧвЁЯABE=ЁЯDBCЃЎ
ЃЈ1ЃЉХаЖЯжБЯпBEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉШєsinЁЯABE=![]() ЃЌCD=2ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌCD=2ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
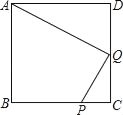
ЁОЬтФПЁПШчЭМЃЌPЪЧе§ЗНаЮABCDБпBCЩЯЕФвЛЕуЃЌЧвBP=3PCЃЌQЪЧCDжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADQЁзЁїQCPЃЎ
ЃЈ2ЃЉЪдЮЪЃКAQгыPQгаЪВУДЙиЯЕЃЈЮЛжУгыЪ§СПЃЉЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com