
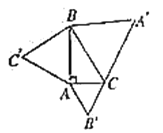
【题目】如图,在![]() 中,
中,![]() 度.以
度.以![]() 的三边为边分别向外作等边三角形
的三边为边分别向外作等边三角形![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() 的面积分别是8和3,则
的面积分别是8和3,则![]() 的面积是( )
的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
【答案】D
【解析】
先设AC=b,BC=a,AB=c,根据勾股定理有c2+b2=a2,再根据等式性质可得![]() c2+
c2+![]() b2=
b2=![]() a2,再根据等边三角形的性质以及特殊三角函数值,易求得S3=
a2,再根据等边三角形的性质以及特殊三角函数值,易求得S3=![]() ×sin60°aa=
×sin60°aa=![]() a2,同理可求S2=
a2,同理可求S2=![]() b2,S1=
b2,S1=![]() c2,从而可得S1+S2=S3,易求S1.
c2,从而可得S1+S2=S3,易求S1.
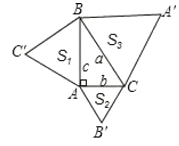
解:如图,设等边三角形△A'BC,△AB'C,△ABC'的面积分别是S3,S2,S1,
设AC=b,BC=a,AB=c,
∵△ABC是直角三角形,且∠BAC=90度,
∴c2+b2=a2,
∴![]() c2+
c2+![]() b2=
b2=![]() a2,
a2,
又∵S3=![]() ×sin60°aa=
×sin60°aa=![]() a2,同理可求S2=
a2,同理可求S2=![]() b2,S1=
b2,S1=![]() c2,
c2,
∴S1+S2=S3,
∵S3=8,S2=3,
∴S1=S3S2=83=5,
故选:D.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,直线 y1 与 y2 相交于点C , y1 与 x 轴交于点 D ,与 y 轴交于点0,1, y2 与 x 轴 交于点 B3,0,与 y 轴交于点 A ,下列说法正确的个数有( )
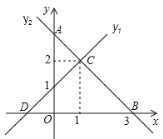
①y1的 解 析 式 为![]() ;② OA OB ;③
;② OA OB ;③![]() ;④
;④![]() ;⑤ AOB BCD .
;⑤ AOB BCD .
A.2 个B.3个C.4 个D.5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
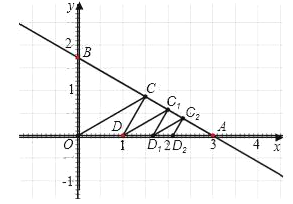
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处(
处(![]() ),一边
),一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.

(1)将图1中的三角板绕点![]() 逆时针旋转至图2,使一边
逆时针旋转至图2,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,求
,求![]() 的度数;
的度数;
(2)将图1中的三角板绕点![]() 以每秒5的速度沿逆时针方向旋转一周,在旋转的过程中,第
以每秒5的速度沿逆时针方向旋转一周,在旋转的过程中,第![]() 秒时,直线
秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() ,求
,求![]() 的值;
的值;
将图1中的三角板绕点![]() 逆时针旋转至图3,使一边
逆时针旋转至图3,使一边![]() 在
在![]() 的内部,请探究
的内部,请探究![]() 的值./span>
的值./span>
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
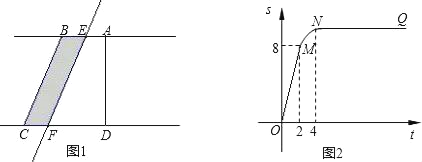
信息读取
(1)梯形上底的长AB= ;
(2)直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
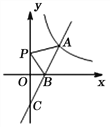
【题目】如图,一次函数y=2x+b的图象与反比例函数![]() (x>0)的图象交于点A(m,2),与坐标轴分别交于B和C(0,-2)两点.
(x>0)的图象交于点A(m,2),与坐标轴分别交于B和C(0,-2)两点.
(1)求反比例函数的表达式;
(2)若P是y轴上一动点,当PA+PB的值最小时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com