
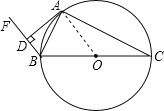
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.

(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)见解析;(2)5
【解析】
试题分析:(1)要证AD是⊙O的切线,连接OA,只证∠DAO=90°即可.
(2)根据三角函数的知识可求出AD,从而根据勾股定理求出AB的长,根据三角函数的知识即可得出⊙O的直径.
(1)证明:连接OA;
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵BD=1,tan∠BAD=![]() ,
,
∴AD=2,
∴AB=![]() =
=![]() ,
,
∴cos∠DBA=![]() ;
;
∵∠DBA=∠CBA,
∴BC=![]() =
=![]() =5.
=5.
∴⊙O的直径为5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
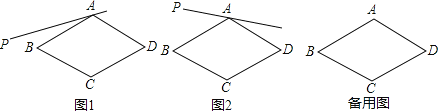
【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2﹣(m+2)x+2(m≠0).
(1)求证:此二次函数的图象与x轴总有交点;
(2)如果此二次函数的图象与x轴两个交点的横坐标都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组线段能组成一个三角形的是( )
A. 4cm,6cm,11cm B. 4cm,5cm,1cm
C. 3cm,4cm,5cm D. 2cm,3cm,6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y=![]() 的图象交于点A(﹣1,n).
的图象交于点A(﹣1,n).
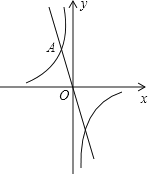
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)请用树状图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出球上的数字的积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)请用树状图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出球上的数字的积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
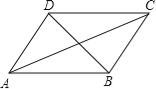
A. 当AC=BD时,四边形ABCD是矩形
B. 当AB=BC时,四边形ABCD是菱形
C. 当AC⊥BD时,四边形ABCD是菱形
D. 当∠DAB=90°时,四边形ABCD是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com