
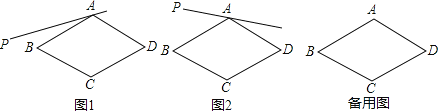
【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
【答案】(1)见解析;(2)∠ABF=∠ADF.见解析;(3)DF=ED﹣BF.见解析;(4)BF=DE+DF.
【解析】
试题分析:(1)根据题目要求补全图形即可;
(2)连接AE.由轴对称图形的性质可知EA=AB,∠ABF=∠AEF,由菱形的定义可知AB=AD,从而得到AE=AD,由等腰三角形的性质可知∠AEF=∠ADF,于是得到∠ABF=∠ADF;
(3)由轴对称图形的性质可知EF=BF,然后由DF=ED﹣EF,可知DF=ED﹣BF;
(4)由轴对称图形的性质可知EF=BF,然后由EF=ED+DF,可知BF=DE+DF.
解:(1)如图1所示:
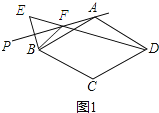
(2)∠ABF=∠ADF.
理由:如图2所示:连接AE.
∵点B与点E关于直线PA对称,
∴EA=AB,∠ABF=∠AEF.
∵四边形ABCD为菱形,
∴AB=AD.
∴AE=AD.
∴∠AEF=∠ADF.
∴∠ABF=∠ADF.
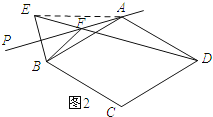
(3)DF=ED﹣BF.
理由:如图3所示:
∵点B与点E关于PA对称,
∴EF=BF.
又∵DF=ED﹣EF,
∴DF=ED﹣BF.
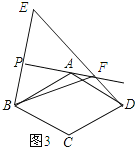
(4)BF=DE+DF.
理由:如图4所示:
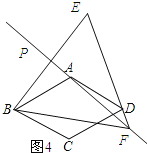
∵点B与点E关于PA对称,
∴EF=BF.
又∵EF=ED+DF,
∴BF=DE+DF.


科目:初中数学 来源: 题型:
【题目】已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.
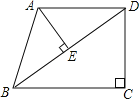
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
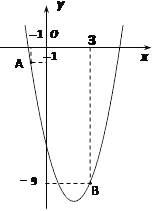
【题目】如图,已知二次函数![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x﹣1)2+4
C.y=(x+1)2+2 D.y=(x﹣1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了“讲文明、守秩序、迎南博”知识竞赛活动,从中抽取了7名同学的参赛成绩如下(单位:分):80,90,70,100,60,80,80.则这组数据的中位数和众数分别是( )
A. 90,80 B. 70,80 C. 80,80 D. 100,80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.

(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com