
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y=![]() 的图象交于点A(﹣1,n).
的图象交于点A(﹣1,n).
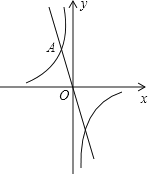
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
【答案】(1)y=﹣![]() ;(2)点P的坐标为(﹣2,0)或(0,4).
;(2)点P的坐标为(﹣2,0)或(0,4).
【解析】
试题分析:(1)先把A(﹣1,n)代入y=﹣2x求出n的值,确定A点坐标为(﹣1,2),然后把A(﹣1,2)代入y=![]() 可求出k的值,从而可确定反比例函数的解析式;
可求出k的值,从而可确定反比例函数的解析式;
(2)过A作AB⊥x轴于点B,AC⊥y轴于点C,则B点坐标为(﹣1,0),C点坐标为(0,2),由于PA=OA,然后利用等腰三角形的性质易确定满足条件的P点坐标.
解:(1)把A(﹣1,n)代入y=﹣2x得n=﹣2×(﹣1)=2,
∴A点坐标为(﹣1,2),
把A(﹣1,2)代入y=![]() 得k=﹣1×2=﹣2,
得k=﹣1×2=﹣2,
∴反比例函数的解析式为y=﹣![]() ;
;
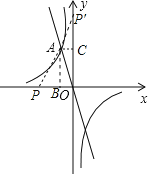
(2)过A作AB⊥x轴于点B,AC⊥y轴于点C,如图,
∵点A的坐标为(﹣1,2),
∴B点坐标为(﹣1,0),C点坐标为(0,2)
∴当P在x轴上,其坐标为(﹣2,0);
当P点在y轴上,其坐标为(0,4);
∴点P的坐标为(﹣2,0)或(0,4).


科目:初中数学 来源: 题型:
【题目】一个正方形在平面直角坐标系中三个顶点的坐标为(-2,-3),(-2,1),(2,1),则第四个顶点的坐标为( )
A. (2,2) B. (3,2) C. (2,-3) D. (2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x﹣1)2+4
C.y=(x+1)2+2 D.y=(x﹣1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.

(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
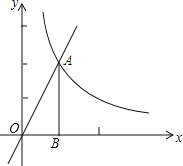
【题目】如图,直线y=2x与双曲线y=![]() 在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
A.(2,0) B.(2,﹣1) C.(﹣2,1) D.(﹣1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )
A.100(1+x)2=81 B.100(1﹣x)2=81
C.100(1﹣x%)2=81 D.100x2=81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的个数是( )
①垂直于半径的直线一定是这个圆的切线;
②圆有且只有一个外切三角形;
③三角形有且只有一个内切圆;
④三角形的内心到三角形的三个顶点的距离相等.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com