Question

8．每个小方格都是边长为1个单位长度，正方形ABCD在坐标系中的位置如图所示．
（1）画出正方形ABCD关于原点中心对称的图形；
（2）画出正方形ABCD绕点D点顺时针方向旋转90°后的图形；
（3）求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线．

Answer 1

分析 （1）根据关于原点中心对称的点的坐标特征写出A、B、C、D的对应点A′、B′、C′、D′的坐标，然后描点即可得到正方形A′B′C′D′；
（2）根据网格特点、正方形的性质和旋转的性质画出点C和B的对应点E和F，则可得到正方形ABCD绕点D点顺时针方向旋转90°后的正方形CFED；
（3）由于点B绕点D点顺时针方向旋转90°后经过的路径为以D点为圆心，半径为BD，圆心角为90度的弧，于是根据弧长公式可求解．

解答 解：（1）如图，正方形A′B′C′D′为所作；
（2）如图，正方形CFED为所作；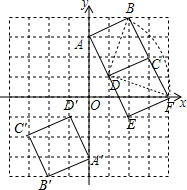

（3）BD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
所以正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线长=$\frac{90•π•\sqrt{10}}{180}$=$\frac{\sqrt{10}}{2}$π．

点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．