
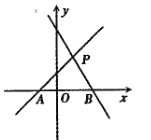
【题目】如图,直线![]() 是一次函数
是一次函数![]() 的图象,直线
的图象,直线![]() 是一次函数
是一次函数![]() 的图象.
的图象.
(1)求A、B、P三点坐标;
(2)求![]() 的面积;
的面积;
(3)已知过P点的直线把![]() 分成面积相等的两部分,求该直线解析式.
分成面积相等的两部分,求该直线解析式.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)3;(3)
;(2)3;(3)![]() .
.
【解析】
(1)把y=0分别代入![]() 、
、![]() 求出x即可得到A、B的坐标,联立两个函数解析式得到方程组,解方程组即可得到点P的坐标;
求出x即可得到A、B的坐标,联立两个函数解析式得到方程组,解方程组即可得到点P的坐标;
(2)根据A、B、P三点的坐标及三角形面积公式即可求解;
(3)设过P点直线交x轴于点D,根据面积相等及两个三角形同高,可知AD=BD,据此求出点D坐标,再利用待定系数法求解析式即可.
解:(1)直线![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() ,
,
直线![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() ,
,
联立函数解析式得方程组![]() ,解得
,解得![]() ,
,
∴![]() ;
;
(2)过P点作PC⊥x轴,垂足为C,
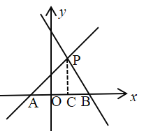
∵![]() ,
,
∴AB=2-(-1)=3,PC=2,
∴S△ABP=![]() ×3×2=3;
×3×2=3;
(3)设过P点直线交x轴于点D,
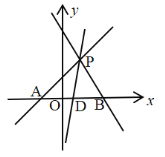
∵S△PAD= S△PBD,且两个三角形同高,
∴AD=BD,
设D点坐标为![]() ,
,
∴![]()
解得![]() ,
,
∴![]() ,
,
设过P、D两点直线解析式为![]() ,则
,则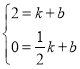 ,
,
解得![]() ,
,
∴直线解析式![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+5的图象与反比例函数y2=![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式;
(2)当y2>y1>0时,写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB上,若BG=![]() -1,则△ABC的周长为( )
-1,则△ABC的周长为( )

A. 4+2![]() B. 6 C. 2+2
B. 6 C. 2+2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均毎天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调査表明:这种冰箱的售价毎降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价![]() 元,商场每天销售这种冰箱的利润为
元,商场每天销售这种冰箱的利润为![]() 元,请写出
元,请写出![]() 与
与![]() 间的函数表达式;(不要求写出自变量的取值范围)
间的函数表达式;(不要求写出自变量的取值范围)
(2)商场要想在这种冰箱销售中毎天盈利4800元,同时又要使百姓得到实惠,毎台冰箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
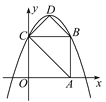
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD=2AB,∠ABC=90°,将△ABC沿BC翻折得到△A′BC,且A′、C、D三点共线,∠A′CB=52°,则∠CAD=( )
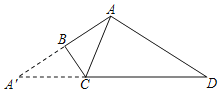
A.78°B.66°C.52°D.38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE是⊙O的切线.
(2)若DE+EA=4,⊙O的半径为5,求CF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
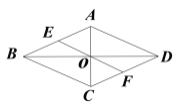
【题目】如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com