
【题目】新华书店销售一个系列的儿童书刊,每套进价100元,定价为140元,一天可以销售20套.为了扩大销售,增加盈利,减少库存,书店决定采取降价措施.若一套书每降价0.5元,平均每天可多售出1套.设每套书降价x元时,书店一天可获利润y元.
(1)求出y与x的函数关系式;
(2)该书店要获得最大利润,售价应定为每套多少元?
(3)小静说:“当某天的利润最大时,当天的销售额也最大.”你认为对吗?请说明理由.
【答案】(1)![]() ;(2)当定价为125元时,该书店获利最大;(3)不对。可以举例说明,如:当单价为125时,销售量为50套,则销售额为6250元,当单价为120时,销售量为60套,则销售额为7200元.
;(2)当定价为125元时,该书店获利最大;(3)不对。可以举例说明,如:当单价为125时,销售量为50套,则销售额为6250元,当单价为120时,销售量为60套,则销售额为7200元.
【解析】
(1)依题意,降价后单套利润为:(140-x-100)元,根据“一套书每降价0.5元,平均每天可多售出1套”,则降价后日销售量为:(20+![]() ),根据总利润=单套利润×销售量,即可得到y与x的关系式.
),根据总利润=单套利润×销售量,即可得到y与x的关系式.
(2)利用关系式中a的值和顶点坐标求最值即可;
(3)举一个反例即可.
解:(1)依题意:![]()
化成一般式得:![]()
(2)∵![]()
∴当![]() 时,y有最大值
时,y有最大值
∴此时的售价为:140-15=125(元)
答:当定价为125元时,该书店获利最大;
(3)当单价为125时,即![]() 时,销售量为(20+
时,销售量为(20+![]() )=50套,
)=50套,
销售额为:125×50=6250元,
当单价为120时,即![]() 时,销售量为(20+
时,销售量为(20+![]() )=60套,
)=60套,
销售额为:120×60=7200元
∵6250元<7200元
∴“当某天的利润最大时,当天的销售额也最大”是错误的.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=﹣![]() (x+2)2﹣2
(x+2)2﹣2
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 .
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线y=﹣![]() x2就可以得到抛物线y=﹣
x2就可以得到抛物线y=﹣![]() (x+2)2﹣2.
(x+2)2﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y=kx+k交x轴负半轴于点A,交y轴正半轴于点B,且AB=2
(1)求k的值;
(2)点P从A出发,以每秒1个单位的速度沿射线AB运动,过点P作直线AB的垂线交x轴于点Q,连接OP,设△PQO的面积为S,点P运动时间为t,求S与t的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,当P在AB的延长线上,若OQ+AB=![]() (BQ﹣OP),求此时直线PQ的解析式.
(BQ﹣OP),求此时直线PQ的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O与点E,连接BE,CE.
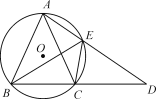
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为______时,四边形AOCE是菱形;
②若AE=![]() ,AB=2
,AB=2![]() ,则DE的长为______.
,则DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=7,将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,点E、F分别是BD、B′D′的中点,则EF的长度为________cm.
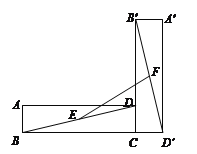
查看答案和解析>>
科目:初中数学 来源: 题型:
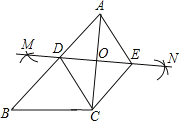
【题目】如图,已知△ABC,按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M,N;
AC的长为半径在AC两边作弧,交于两点M,N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形.
(2)当∠ACB=90°,AC=16,△ADC的周长为36时,直接写出四边形ADCE的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中装有四个完全相同的小球,它们分别写有“美”“丽”、“椒”、“江”的文字.
(1)先从袋摸出1个球后放回,混合均匀后再摸出1个球,求两次摸出的球上是写有“美丽”二字的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球。求两次摸出的球上写有“椒江”二字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳阳超市以每件10元的价格购进了一批玩具,定价为20元时,平均每天可售出80个.经调查发现,玩具的单价每降1元,每天可多售出40个;玩具的单价每涨1元,每天要少售出5个.如何定价才能使每天的利润最大?求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
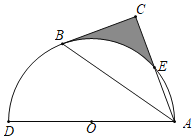
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E;B、E是半圆弧的三等分点,![]() 的长为
的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com