
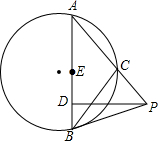
 如图所示,AB是⊙O的一条弦,P是⊙O外一点,PB切⊙P于B,PA交⊙O于点C,且AC=BC,PD⊥AB于D,E是AB的中点,求证:PB=2DE.
如图所示,AB是⊙O的一条弦,P是⊙O外一点,PB切⊙P于B,PA交⊙O于点C,且AC=BC,PD⊥AB于D,E是AB的中点,求证:PB=2DE. 分析 连接EC,根据等腰三角形三线合一的性质得出CE⊥AB,即可证得CE∥PD,根据平行线分相等成比例定理得出$\frac{AE}{DE}$=$\frac{AC}{PC}$=$\frac{BC}{PC}$,然后证得△BPC∽△APB,得出$\frac{BC}{PC}$=$\frac{AB}{PB}$,即可得出$\frac{AE}{DE}$=$\frac{AB}{PB}$,根据AB=2AE,即可证得结论.
解答 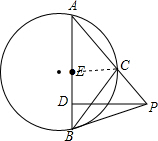 证明:连接EC,
证明:连接EC,
∵AC=BC,E是AB的中点,
∴CE⊥AB,
∵PD⊥AB,
∴CE∥PD,
∴$\frac{AE}{DE}$=$\frac{AC}{PC}$,
∴$\frac{AE}{DE}$=$\frac{AC}{PC}$=$\frac{BC}{PC}$,
∵PB切⊙P于B,
∴∠PBC=∠A,
∵∠BPC=∠APB,
∴△BPC∽△APB,
∴$\frac{BC}{PC}$=$\frac{AB}{PB}$,
∴$\frac{AE}{DE}$=$\frac{AB}{PB}$,
∵AB=2AE,
∴PB=2DE.
点评 本题考查了切线的性质,等腰三角形的性质,平行线的判定和性质,三角形相似的判定和性质,作出辅助线构,证得平行线是解题的关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:单选题
有五只灯泡,其中两只是次品,从中任取一只恰为合格品的概率为( )
A. 20% B. 40% C. 50% D. 60%
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
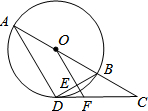 如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.
如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
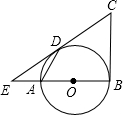 如图,AB为⊙O的直径,CB、CD分别与⊙O相切于B、D,延长BA、CD交于E,连接AD,DE=4,BE=8.
如图,AB为⊙O的直径,CB、CD分别与⊙O相切于B、D,延长BA、CD交于E,连接AD,DE=4,BE=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
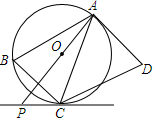 如图,四边形ABCD是平行四边形,⊙O是△ABC的外接圆,AD与⊙O相切于点A,AO的延长线与过点C的直线相交于点P,且∠PCB=∠ACD.
如图,四边形ABCD是平行四边形,⊙O是△ABC的外接圆,AD与⊙O相切于点A,AO的延长线与过点C的直线相交于点P,且∠PCB=∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
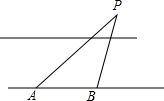 在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)
在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com