
【题目】如图,在平面直角坐标系中,△AOB是边长为2的等边三角形,将△AOB绕着点B按顺时针方向旋转得到△DCB,使得点D落在x轴的正半轴上,连接OC,AD.
(1)求证:OC=AD;
(2)求OC的长.

【答案】(1)证明见解析;(2)OC=2![]() .
.
【解析】
(1)已知△DCB是由△AOB绕着点B按顺时针方向旋转得到的,可得△DCB也是边长为2的等边三角形,再证明△OBC≌△ABD,根据全等三角形的性质即可证得结论;(2)根据等边三角形的性质、等腰三角形的性质及三角形的内角和定理求得∠OCD=90°,在Rt△OCD中,OD=4,CD=2,由勾股定理即可求得CO的长.
(1)证明:∵△AOB是边长为2的等边三角形,
∴OA=OB=AB=2,∠AOB=∠BAO=∠OBA=60°,
又∵△DCB是由△AOB旋转得到的,
∴△DCB也是边长为2的等边三角形,
∴∠OBA=∠CBD=60°,BC=BD,
又∠OBC=∠OBA+∠ABC=∠CBD+∠ABC=∠ABD,
在△OBC和△ABD中,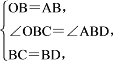
∴△OBC≌△ABD(SAS),
∴OC=AD.
(2)∵△AOB与△BCD是边长为2的等边三角形,
∴BO=BC,∠OBA=∠DBC=∠BCD=60°,
∴∠OBC=120°,
∴∠BOC=∠BCO=30°,
∴∠OCD=90°.
∵OD=4,CD=2,
∴在Rt△OCD中,由勾股定理,得OC=![]() =
=![]() =2
=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数.
(2)设∠BAD=θ,当θ为何值时,△DFG为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′B′C′成中心对称,下列说法不正确的是( )

A. S△ABC=S△A′B′C′ B. AB=A′B′,AC=A′C′,BC=B′C′
C. AB∥A′B′,AC∥A′C′,BC∥B′C′ D. S△ACO=S△A′B′O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中有一个四边形图案.
(1)请你分别画出△ABC绕点O顺时针旋转90°的图形,关于点O对称的图形以及逆时针旋转90°的图形,并将它们涂黑;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算、化简
(1)y2·y3·y4
(2)(-4a2b)3
(3) (22)4×(![]() )8
)8
(4)-8-(-15)+(-9)-(-12);
(5)![]() ;
;
(6)[-22-(![]() )×36]÷5;
)×36]÷5;
(7)(-1)2017-![]() ];
];
(8)5(3a2b-ab2)-4(-ab2+3a2b);
(9)(2x2y+2xy2)-[2(x2y-1)+3xy2+2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]()
![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() 、
、![]() 两点,已知点
两点,已知点![]() ,点
,点![]() .
.
(1)求直线和双曲线的解析式;
(2)把直线![]() 沿
沿![]() 轴负方向平移2个单位后得到直线
轴负方向平移2个单位后得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量被池塘相隔的两棵树![]() ,
,![]() 的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树
的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树![]() 沿着垂直于
沿着垂直于![]() 的方向走到
的方向走到![]() ,再从
,再从![]() 沿着垂直于
沿着垂直于![]() 的方向走到
的方向走到![]() ,
,![]() 为
为![]() 上一点,其中
上一点,其中![]() 位同学分别测得三组数据:
位同学分别测得三组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中能根据所测数据求得
,其中能根据所测数据求得![]() ,
,![]() 两树距离的有( )
两树距离的有( )
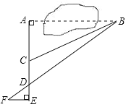
A. 0组 B. 一组 C. 二组 D. 三组
查看答案和解析>>
科目:初中数学 来源: 题型:
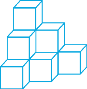
【题目】如图是由若干个完全相同的小正方体堆成的几何体.
(1)画出该几何体的三视图;
(2)在该几何体的表面喷上红色的漆,则在所有的小正方体中,有几个正方体的三个面是红色?
(3)若现在你手头还有一个相同的小正方体.
a.在不考虑颜色的情况下,该正方体应放在何处才能使堆成的几何体的三视图不变?直接在图中添上该正方体;
b.若考虑颜色,要使三视图不变,则新添的正方体至少要在几个面上着色?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com