
【题目】如图,在平面直角坐标系中,直线![]()
![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() 、
、![]() 两点,已知点
两点,已知点![]() ,点
,点![]() .
.
(1)求直线和双曲线的解析式;
(2)把直线![]() 沿
沿![]() 轴负方向平移2个单位后得到直线
轴负方向平移2个单位后得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】雪枫中学食堂一工人在每天摆碗的过程中总结出,如果你给他报出桌面上碗的高度,他能说出碗的个数,你给他报出碗的个数他能说出确的高度,真可谓数学就在身边,缺乏慧眼发现:

(1)求整齐叠放在桌面上碗的高度y(cm)与碗数x(个)之间的一次函数解析式(不要求写出自变量 x的取值范围):
(2)若桌面上有12个碗,整齐叠放成一摞,求出它的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,二次函数
与x轴交于点B,与y轴交于点C,二次函数![]() 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB是边长为2的等边三角形,将△AOB绕着点B按顺时针方向旋转得到△DCB,使得点D落在x轴的正半轴上,连接OC,AD.
(1)求证:OC=AD;
(2)求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程![]() 的两个根是
的两个根是![]() ,
,![]() ,那么
,那么![]() ,
,![]() .请根据以上结论,解决下列问题:
.请根据以上结论,解决下列问题:
![]() 已知关于
已知关于![]() 的方程
的方程![]() ,求出一个一元二次方程,使它的两根别是已知方程两根的倒数;
,求出一个一元二次方程,使它的两根别是已知方程两根的倒数;
![]() 已知
已知![]() 、
、![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
![]() 已知
已知![]() 、
、![]() 、
、![]() 均为实数,且
均为实数,且![]() ,
,![]() ,求正数
,求正数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某林场计划修一条长![]() ,断面为等腰梯形的渠道,断面面积为
,断面为等腰梯形的渠道,断面面积为![]() ,上口宽比渠深多
,上口宽比渠深多![]() ,渠底比渠深多
,渠底比渠深多![]()
![]() 渠道的上口宽与渠底宽各是多少?
渠道的上口宽与渠底宽各是多少?
![]() 如果计划每天挖土
如果计划每天挖土![]() ,需要多少天才能把这条渠道挖完?
,需要多少天才能把这条渠道挖完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
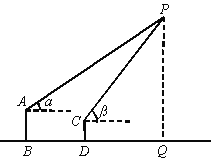
【题目】如图,爸爸和小莉在两处观测气球的仰角分别为α、β,两人的距离(BD)是100 m, 如果爸爸的眼睛离地面的距离(AB)为1.6 m,小莉的眼睛离地面的距离(CD)为1.2 m,那么气球的高度(PQ)是多少?(用含α、β的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com