
【题目】在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,二次函数
与x轴交于点B,与y轴交于点C,二次函数![]() 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.

【答案】(1)二次函数的表达式为:![]() ;(2)4;(3)
;(2)4;(3)![]() 或
或![]() .
.
【解析】
(1)先求得点B、C的坐标,再代入![]() 求得b、c的值,即可得二次函数的表达式;(2)过点
求得b、c的值,即可得二次函数的表达式;(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,则
,则![]() .用含有a的代数式表示出
.用含有a的代数式表示出![]() 的长,再根据
的长,再根据![]() 得到S与a的二次函数关系,利用二次函数的性质即可解答;(3)在x轴上取点K,使CK=BK,则∠OKC=2∠ABC,过点B作BQ∥MD交CD延长线于点Q,过点Q作QH⊥x轴于点H,分∠DCM=∠QCB=2∠ABC和∠CDM=∠CQB=2∠ABC两种情况求点D的横坐标即可.
得到S与a的二次函数关系,利用二次函数的性质即可解答;(3)在x轴上取点K,使CK=BK,则∠OKC=2∠ABC,过点B作BQ∥MD交CD延长线于点Q,过点Q作QH⊥x轴于点H,分∠DCM=∠QCB=2∠ABC和∠CDM=∠CQB=2∠ABC两种情况求点D的横坐标即可.
(1)直线![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() .
.
∵二次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,
两点,
∴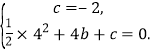 解得
解得
∴二次函数的表达式为:![]() .
.
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
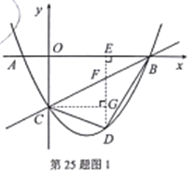
依题意设![]() ,则
,则![]() .
.
其中![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∵![]() ,∴抛物线开口向下.
,∴抛物线开口向下.
又∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() ;
;
(3)![]() 或
或![]()
在![]() 轴上取点
轴上取点![]() ,使
,使![]() ,则
,则![]() .
.
过点![]() 作
作![]() ∥
∥![]() 交
交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
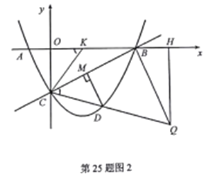
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,解得
,解得![]() .∴
.∴![]() .
.
当![]() 时,
时,
∴![]() .
.
∴![]() .
.
易证![]() ∽
∽![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴直线![]() 的函数表达式为:
的函数表达式为:![]() .
.
由![]() ,解得:
,解得:![]() ,
,![]() (舍).
(舍).
∴![]() 点的横坐标为2.
点的横坐标为2.
②当![]() 时,方法同①,可确定点
时,方法同①,可确定点![]() 的横坐标为
的横坐标为![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
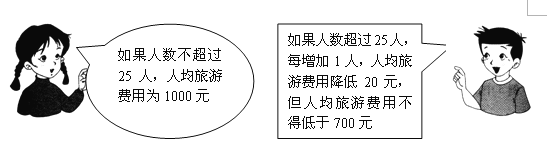 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数.
(2)设∠BAD=θ,当θ为何值时,△DFG为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元.经调查发 现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:

(1)求y与x之间的函数关系式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′B′C′成中心对称,下列说法不正确的是( )

A. S△ABC=S△A′B′C′ B. AB=A′B′,AC=A′C′,BC=B′C′
C. AB∥A′B′,AC∥A′C′,BC∥B′C′ D. S△ACO=S△A′B′O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中有一个四边形图案.
(1)请你分别画出△ABC绕点O顺时针旋转90°的图形,关于点O对称的图形以及逆时针旋转90°的图形,并将它们涂黑;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]()
![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() 、
、![]() 两点,已知点
两点,已知点![]() ,点
,点![]() .
.
(1)求直线和双曲线的解析式;
(2)把直线![]() 沿
沿![]() 轴负方向平移2个单位后得到直线
轴负方向平移2个单位后得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①四边形ABCD是平行四边形,线段EF分别交AD、AC、BC于点E、O、F,②EF⊥AC,③AO=CO.
(1)求证:四边形AFCE是平行四边形;

(2)在本题①②③三个已知条件中,去掉一个条件,(1)的结论依然成立,这个条件是 (直接写出这个条件的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com