
【题目】如图,①四边形ABCD是平行四边形,线段EF分别交AD、AC、BC于点E、O、F,②EF⊥AC,③AO=CO.
(1)求证:四边形AFCE是平行四边形;

(2)在本题①②③三个已知条件中,去掉一个条件,(1)的结论依然成立,这个条件是 (直接写出这个条件的序号).
【答案】(1)证明见解析(2)②
【解析】分析:(1)根据平行四边形的性质可得AE∥CF,根据平行线的性质可得∠DAC=∠BCA,然后再加上条件AO=CO,对顶角∠AOE=∠FOC,可利用ASA证明△AOE≌△COF,根据全等三角形的性质可得AE=CF,根据一组对边平行且相等的四边形是平行四边形即可得四边形AFCE是平行四边形;(2)根据(1)的证明可得EF⊥AC多余.
详解:
(1)∵四边形ABCD是平行四边形,
∴AE∥CF,
∴∠DAC=∠BCA ,
在△AOE和△COF中, 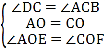 ,
,
∴△AOE≌△COF(ASA)
∴AE=CF
∴四边形AFCE是平行四边形
(2)由(1)的证明可得EF⊥AC多余.
故答案为:②.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,二次函数
与x轴交于点B,与y轴交于点C,二次函数![]() 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某林场计划修一条长![]() ,断面为等腰梯形的渠道,断面面积为
,断面为等腰梯形的渠道,断面面积为![]() ,上口宽比渠深多
,上口宽比渠深多![]() ,渠底比渠深多
,渠底比渠深多![]()
![]() 渠道的上口宽与渠底宽各是多少?
渠道的上口宽与渠底宽各是多少?
![]() 如果计划每天挖土
如果计划每天挖土![]() ,需要多少天才能把这条渠道挖完?
,需要多少天才能把这条渠道挖完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6,P是直线AB上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B/CP,连接B/A,B/A长度的最小值是m,B/A长度的最大值是n,则m+n的值等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市水果货架上有四个苹果,重量分别是100 g、110 g、120 g和125 g.
(1)小明妈妈从货架上随机取下一个苹果.恰是最重的苹果的概率是 ;
(2)小明妈妈从货架上随机取下两个苹果.它们总重量超过232 g的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,爸爸和小莉在两处观测气球的仰角分别为α、β,两人的距离(BD)是100 m, 如果爸爸的眼睛离地面的距离(AB)为1.6 m,小莉的眼睛离地面的距离(CD)为1.2 m,那么气球的高度(PQ)是多少?(用含α、β的式子表示)
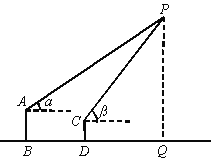
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于E,BD⊥CF,AF⊥CF,则下列结论:①∠ACF=∠CBD②BD=FC③FC=FD+AF④AE=DC中,正确的结论是____________(填正确结论的编号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com