
【题目】已知:如图,A、C、F、D在同一直线上,AF=DC,AB∥DE,AB=DE.
求证:(1) △ABC≌△DEF;
(2)BC∥EF.

科目:初中数学 来源: 题型:
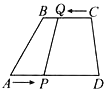
【题目】如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,AD=9 cm.点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动,当点P,Q运动_______s时,直线QP将四边形截出一个平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在平面直角坐标系中的圆O的半径为3,现做如下实验:抛掷一枚均匀的正四面体骰子,它有四个顶点,各顶点数分别是1,2,3,4,每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标). 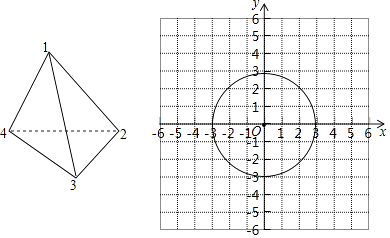
(1)若第一次骰子朝上的点数为1,第二次骰子朝上的点数为2,此时点P(填“是”或“否”)落在圆O内部;
(2)请你用树状图或列表的方法表示出P点坐标的所有可能结果;
(3)求点P落在圆O面上(含内部与边界)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)先阅读下面的例题,再按要求完成下列问题.
例:解不等式(x-2)(x+1)>0.
解:由有理数的乘法法则“两数相乘,同号得正”,得①![]() 或②
或②![]()
解不等式组①,得x>2.
解不等式组②,得x<-1.
所以不等式(x-2)(x+1)>0的解集为x>2或x<-1.
解不等式:(1)![]() >0;(2)
>0;(2) ![]() <0.
<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家居专营店用2730元购进A、B两种新型玻璃保温杯共60个,这两种玻璃保温杯的进价、标价如表所示:
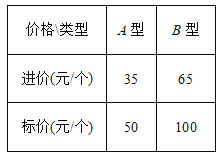
(1)这两种玻璃保温杯各购进多少个?
(2)若A型玻璃保温杯按标价的9折出售,B型玻璃保温杯按标价的8.5折出售,且在运输过程中有2个A型、1个B型玻璃保温杯不慎损坏,不能进行销售,请问这批玻璃保温杯全部售出后,该家居专营店共获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com