
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于点C(0,5).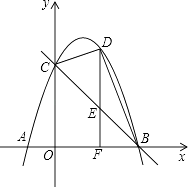
(1)求该抛物线所对应的函数关系式;
(2)D是笫一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD.设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围;
②当m为何值时,S有最大值,并求这个最大值;
③直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A、B、C三个点,它们表示的数分别是![]() 、
、![]() 、
、![]() 。
。

(1)填空:AB= ,BC= ;
(2)现有动点M、N都从A点出发,点M以每秒2个单位长度的速度向右移动,当点M移动到B点时,点N才从A点出发,并以每秒3个单位长度的速度向右移动,求点N移动多少时间,点N追上点M?
(3)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动。试探索:BC-AB的值是否随着时间的变化而改变?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: y= ![]() .
.
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本) 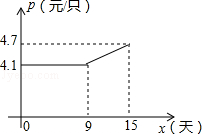
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△P1OA1 , △P2A1A2都是等腰直角三角形,点P1 , P2都在函数y= ![]() (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( ) 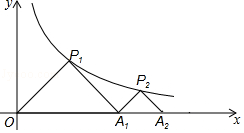
A.(4 ![]() ,
, ![]() )
)
B.(4+2 ![]() ,4﹣2
,4﹣2 ![]() )??
)??
C.(2+2 ![]() ,2
,2 ![]() ﹣2)
﹣2)
D.(4+2 ![]() ,2+2
,2+2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=12cm,
(1)求线段CD的长;
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 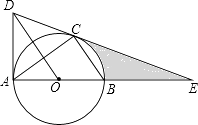
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=6,CE=2 ![]() . ①求⊙O的半径
. ①求⊙O的半径
②求线段CE,BE与劣弧 ![]() 所围成的图形的面积(结果保留根号和π)
所围成的图形的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+3交y轴于点A,交x轴正半轴于点C(3,0),交x轴负半轴于点B(﹣1,0),∠ACB=45°.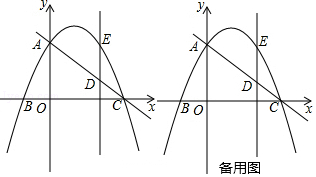
(1)求此抛物线的解析式;
(2)点D为线段AC上一点,且AD=2CD,过点D作DE∥y轴,交抛物线一点E,点P为x轴上方抛物线的一点,设点P的横坐标为t,△PDE的面积为s,求s与t之间的函数关系式,并直接写出t的范围;
(3)在(2)的条件下,过点P作PF∥DE交直线AC于点F,是否存在点P,使以点P、F、E、D为顶点的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)若点D与点A重合,则这个操作过程为FZ[ , ];
(2)若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com