
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.

【答案】(1)BC=2;(2)见解析;
【解析】试题分析:
(1)由已知条件根据“垂径定理”易得AP=CP=![]() AC=
AC=![]() ,结合OA=3可得OP=1,结合AB是⊙O的直径可得OP=
,结合OA=3可得OP=1,结合AB是⊙O的直径可得OP=![]() BC,由此可得BC=2;
BC,由此可得BC=2;
(2)由OG=9,OA=3,OB=3,OP=1,可得![]() ,结合∠BOG=∠POA,可得△BOG∽△POA,从而可得∠GBO=∠OPA=90°,由此可得得到FG是⊙O的切线.
,结合∠BOG=∠POA,可得△BOG∽△POA,从而可得∠GBO=∠OPA=90°,由此可得得到FG是⊙O的切线.
试题解析:
(1)∵DE是⊙O的直径,且DE⊥AC,
∴AP=PC=![]() AC=
AC=![]() ,
,
又∵OA=3,
∴OP=1
又AB是⊙O的直径,
∴O为AB的中点,
∴OP=![]() BC,
BC,
∴BC=2OP=2.
(2)∵OG=9,OA=3,OB=3,OP=1,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∠BOG=∠POA,
∴△BOG∽△POA,
∴∠GBO=∠OPA=90°
又∵点B在⊙O上,
∴FG是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数.
(2)设∠BAD=θ,当θ为何值时,△DFG为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]()
![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() 、
、![]() 两点,已知点
两点,已知点![]() ,点
,点![]() .
.
(1)求直线和双曲线的解析式;
(2)把直线![]() 沿
沿![]() 轴负方向平移2个单位后得到直线
轴负方向平移2个单位后得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量被池塘相隔的两棵树![]() ,
,![]() 的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树
的距离,数学课外兴趣小组的同学们设计了如图所示的测量方案:从树![]() 沿着垂直于
沿着垂直于![]() 的方向走到
的方向走到![]() ,再从
,再从![]() 沿着垂直于
沿着垂直于![]() 的方向走到
的方向走到![]() ,
,![]() 为
为![]() 上一点,其中
上一点,其中![]() 位同学分别测得三组数据:
位同学分别测得三组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中能根据所测数据求得
,其中能根据所测数据求得![]() ,
,![]() 两树距离的有( )
两树距离的有( )
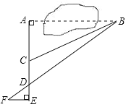
A. 0组 B. 一组 C. 二组 D. 三组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
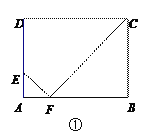
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①四边形ABCD是平行四边形,线段EF分别交AD、AC、BC于点E、O、F,②EF⊥AC,③AO=CO.
(1)求证:四边形AFCE是平行四边形;

(2)在本题①②③三个已知条件中,去掉一个条件,(1)的结论依然成立,这个条件是 (直接写出这个条件的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
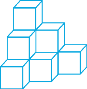
【题目】如图是由若干个完全相同的小正方体堆成的几何体.
(1)画出该几何体的三视图;
(2)在该几何体的表面喷上红色的漆,则在所有的小正方体中,有几个正方体的三个面是红色?
(3)若现在你手头还有一个相同的小正方体.
a.在不考虑颜色的情况下,该正方体应放在何处才能使堆成的几何体的三视图不变?直接在图中添上该正方体;
b.若考虑颜色,要使三视图不变,则新添的正方体至少要在几个面上着色?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用配方法求出抛物线![]() 的顶点坐标、对称轴、最大值或最小值;若将抛物线
的顶点坐标、对称轴、最大值或最小值;若将抛物线![]() 先向左平移
先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得抛物线的函数关系式为________.
个单位,所得抛物线的函数关系式为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com