
【题目】如图①,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
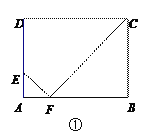
(1)当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
(2)如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)

(3)对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
【答案】(1)AF=1或3;(2)见解析;(3)当1<m<4且m≠3时,有3个;
当m=3时,有2个;当m=4时,有2个; 当m>4时,有1个.
【解析】试题分析:
(1)由题意可知,∠A=∠B=90°,由此可知要使△AEF与△BCF相似,存在两种情况:①当∠AEF=∠BFC时,若![]() ,则两三角形相似;②当∠AEF=∠BCF时, 若
,则两三角形相似;②当∠AEF=∠BCF时, 若![]() ,则两三角形相似;由这两种情况分别根据已知条件进行计算即可得到相应的AF的值;
,则两三角形相似;由这两种情况分别根据已知条件进行计算即可得到相应的AF的值;
(2)如下图所示:①延长DA到E′,使AE′=AE,连接CE′交AB于点F1;②连接CE,以CE为直径作圆,分别交AB于点F2、F3;则F1、F2、F3为所求点;
(3)结合(1)(2)可知,当m=3时,符合条件的点F有2个,当m=4时,符合条件的点F也有2个,而当1<m<4,且 m≠3时,符合条件的点F有3个;而当m>4时,以CE为直径的圆和AB相离,此时符合条件的点F只有1个.
试题解析:
(1)①当∠AEF=∠BFC时,
要使△AEF∽△BFC,需![]() ,即
,即![]() ,
,
解得AF=1或3;
②当∠AEF=∠BCF时,
要使△AEF∽△BCF,需![]() =
=![]() ,即
,即![]() ,
,
解得AF=1;
综上所述AF=1或3
(2)如下图所示,图中F1、F2、F3为所求点;

(提示:延长DA,作点E关于AB的对称点E′,连结CE′,交AB于点F1;连结CE,以CE为直径作圆交AB于点F2、F3);
(3)如(2)中所作图形,
当m=4时,由已知条件可得DE=3,则CE=5,即图中圆的直径为5,由梯形中位线定理可得此时图中所作圆的圆心到AB的距离=2.5=所作圆的半径,F2和F3重合,即当m=4时,符合条件的F有2个;
当m>4时,图中所作圆和AB相离,此时F2和F3不存在了,即此时符合条件的F只有F11个;
而当1<m<4且m≠3时,由所作图形可知,符合条件的F有3个;
综上所述:可得:①当1<m<4且m≠3时,符合条件的F有3个; ②当m=3时,符合条件的F有2个;③当m=4时,符合条件的F有2个;④当m>4时,符合条件的F有1个.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,点O时∠CAB、∠ACB平分线的交点,且BC=8 cm,AB=6 cm,AC=10 m,则点O到边AB的距离为( )

A.1 cmB.2 cmC.3 cmD.4 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程![]() 的两个根是
的两个根是![]() ,
,![]() ,那么
,那么![]() ,
,![]() .请根据以上结论,解决下列问题:
.请根据以上结论,解决下列问题:
![]() 已知关于
已知关于![]() 的方程
的方程![]() ,求出一个一元二次方程,使它的两根别是已知方程两根的倒数;
,求出一个一元二次方程,使它的两根别是已知方程两根的倒数;
![]() 已知
已知![]() 、
、![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
![]() 已知
已知![]() 、
、![]() 、
、![]() 均为实数,且
均为实数,且![]() ,
,![]() ,求正数
,求正数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为3的⊙O中,AB是直径,AC是弦,且AC=4![]() .过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
.过点O作直径DE⊥AC,垂足为点P,过点B的直线交AC的延长线和DE的延长线于点F、G.
(1)求线段AP、CB的长;
(2)若OG=9,求证:FG是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为________(用含a的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市水果货架上有四个苹果,重量分别是100 g、110 g、120 g和125 g.
(1)小明妈妈从货架上随机取下一个苹果.恰是最重的苹果的概率是 ;
(2)小明妈妈从货架上随机取下两个苹果.它们总重量超过232 g的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-![]() x+8的图像与x轴、y轴分别交于A、B两点.P是x轴上一个动点,若沿BP将△OBP翻折,点O恰好落在直线AB上的点C处,则点P的坐标是______.
x+8的图像与x轴、y轴分别交于A、B两点.P是x轴上一个动点,若沿BP将△OBP翻折,点O恰好落在直线AB上的点C处,则点P的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 过
过![]() 轴上的点
轴上的点![]() ,且与抛物线
,且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 点坐标为
点坐标为![]() .
.
![]() 求直线和抛物线所表示的函数表达式;
求直线和抛物线所表示的函数表达式;
![]() 在抛物线上是否存在一点
在抛物线上是否存在一点![]() ,使得
,使得![]() ?若不存在,说明理由;若存在,请求出点
?若不存在,说明理由;若存在,请求出点![]() 的坐标,与同伴交流.
的坐标,与同伴交流.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com