
����Ŀ�����ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ�������ֻ�ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=����멁�����ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
���𰸡�
��1��
�⣺������֪�����۹��ȫ���������0��x��100��
��50x��1100��0��
���x��22��
�֡�x��5�ı�����
��ÿ���������������ӦΪ25Ԫ
��2��
�⣺��ÿ�����ľ�����ΪyԪ��
��0��x��100ʱ��y1=50x��1100��
��y1��x�����������
�൱x=100ʱ��y1�����ֵΪ50��100��1100=3900��
��x��100ʱ��
y2=��50�� ![]() ��x��1100
��x��1100
=�� ![]() x2+70x��1100
x2+70x��1100
=�� ![]() ��x��175��2+5025��
��x��175��2+5025��
��x=175ʱ��y2�����ֵΪ5025��
5025��3900��
�ʵ�ÿ�����������Ϊ175Ԫʱ��ÿ��ľ����������5025Ԫ
����������1���۹ȫ�����ÿ��ľ�����=�������г��������멁�����ѣ����ݲ��ȹ�ϵ��������Ϊ�����г�����ʽ��⼴�ɣ���2���ɺ�������ʽ�Ƿֶκ�������ÿһ��������������ֵ���Ƚϵó����������ֵ�������÷ֶκ���ģ�Ϳ�����һ�κ��������κ�����������Ӧ�ã��������Ĺؼ���Ū�����⣬�����շѷ�ʽ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A�͵�B����C��D�ֱ�Ϊ�߶�AB��OB���е㣬��PΪOA��һ���㣬PC+PDֵ��Сʱ��P������Ϊ�� ��
��x�ᡢy��ֱ��ڵ�A�͵�B����C��D�ֱ�Ϊ�߶�AB��OB���е㣬��PΪOA��һ���㣬PC+PDֵ��Сʱ��P������Ϊ�� ��

A������3��0�� B������6��0�� C����![]() ��0�� D����
��0�� D����![]() ��0��
��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����(��ΪA)������ѧ��ѧУ(��ΪB)�����(��ΪC)����������һ����������Ĵ���ϣ�С����λ��ѧУ����250�״������λ��ѧУ����100�״���С�������ѧ����������飬Ȼ��ؼҳ����緹������ֱ��ȥѧУ�ϿΣ�
(1)���������ʾ��С����(A)��ѧУ(B)�����(C)��λ�ã�
(2)�����С���������ľ��룻
(3)С���������ѧ��У��������ѧ��Уһ�����˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��l��y=x��1��x�ύ�ڵ�A1 �� ��ͼ��ʾ������������A1B1C1O��������A2B2C2C1������������AnBnCnCn��1 �� ʹ�õ�A1��A2��A3������ֱ��l�ϣ���C1��C2��C3������y���������ϣ����Bn�������� �� 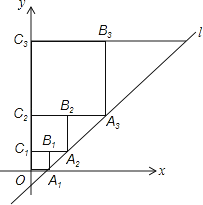
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ���ڵ����ϵĵ��߸�AB��������������ˮƽ����������ϵ�Ӱ�ӷֱ���BC��CD�����BC=6�ף�CD=4�ף���BCD=150�㣬��D����õ��߸˶���A������Ϊ30�㣬������߸˵ĸ߶ȣ�����������ţ�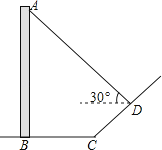
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����BD�����������ӳ����ֱ�����E�͵�F����ʹBE=DF��
��1����֤���ı���AECF�����Σ�
��2����AC=4��BE=1��ֱ��д������AECF�ı߳���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С÷�����ij��Ӱ������վʱ�������������ע���ļס��ҡ���������Ӱ����վͨ���Թ��ڵij������飬�õ���������Ӱ����������ͳ��ͼ�ֱ����£�
�ס��ҡ���������Ӱ�������ͳ��ͼ
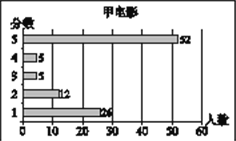


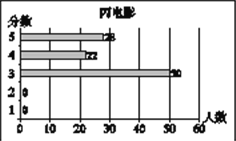
�������ϲ��ϻش��������⣺
��1��С÷������ѧ��ͳ��֪ʶ��������ͳ��ͼ�е����ݽ����˷�������ͨ������õ���������Ӱ��������������������������ֵ�ƽ��������������λ�������㽫�±�����������
�ס��ҡ���������Ӱ�������ͳ�Ʊ�
��Ӱ | �������� | ƽ���� | ���� | ��λ�� |
�� | 100 | 3.45 | 5 | |
�� | 3.66 | 5 | ||
�� | 100 | 3 | 3.5 |
��2������ͳ��ͼ��ͳ�Ʊ��е����ݣ������ƶ�����_______��Ӱ��ԱȽ��ܻ�ӭ��������
_______________________________________________________________________�������ٴ�������ͬ�ĽǶ�˵�����ƶϵĺ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������� ![]() ��
�� ![]() �ύ��A��B���㣨��A�ڵ�B����ࣩ����B������Ϊ��3,0������
�ύ��A��B���㣨��A�ڵ�B����ࣩ����B������Ϊ��3,0������ ![]() �ύ�ڵ�C��0,-3��������ΪD��
�ύ�ڵ�C��0,-3��������ΪD��
��1���������ߵĽ���ʽ������D�����ꡣ
��2������AC��BC�����ACB������ֵ��
��3����P��x����һ�㣬�Ƿ���ڵ�Pʹ�á�PBD���CAB���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɡ�
��4��M����������һ�㣬��N�� ![]() �ᣬ�Ƿ���ڵ�N��ʹ���Ե�A��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɡ�
�ᣬ�Ƿ���ڵ�N��ʹ���Ե�A��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
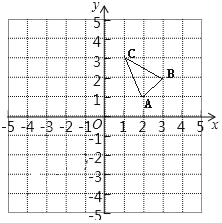
����Ŀ���ڱ߳�Ϊ1����λ���ȵ������������н�����ͼ��ʾ��ƽ��ֱ������ϵ����ABC�Ķ��㶼�ڸ���ϣ������������⣺
��1��������ABC����ƽ��4����λ���Ⱥ�õ��ġ�A1B1C1����д����C1�����ꣻ
��2������A1B1C1��ԭ��O��ʱ����ת90���õ���A2B2C2���뻭����ת��ġ�A2B2C2����д����C2�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com