
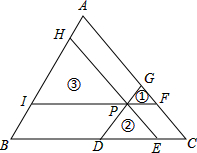
 如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③.已知△ABC的面积的为36,小三角形①、②面积分别为1、4,则小三角形③的面积为9.
如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③.已知△ABC的面积的为36,小三角形①、②面积分别为1、4,则小三角形③的面积为9. 分析 由过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③,得到△GPF∽△PDE∽△HIP,△GPF∽△GDC,△GPF∽△AIF,△HIP∽△HBE,然后由相似三角形面积比等于相似比的平方,求得它们边长比为1:2:3,继而求得答案.
解答 解:过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③,
设小三角形③的面积为x2,
∴△GPF∽△PDE∽△HIP,△GPF∽△GDC,△GPF∽△AIF,△HIP∽△HBE,
∴它们边长比为1:2:x,
∴S△GPF:S△GDC=1:9,S△GPF:S△AIF=1:16,S△HIP:S△HBE=x2:25,
∴S四边形FPEC=9-1-4,S四边形AHPG=16-1-x2,S△HBE=25,
∴S△ABC=S四边形FPEC+S四边形AHPG+S△HBE+S△GPF=9-1-4+16-1-x2+25+1=36.
∴x2=9,
∴小三角形③的面积为9,
故答案为:9.
点评 此题考查了相似三角形的判定与性质.此题难度适中,注意掌握相似三角形面积的比等于相似比的平方定理的应用.


科目:初中数学 来源: 题型:选择题
| A. | 320<x<340 | B. | 320≤x<340 | C. | 320<x≤340 | D. | 320≤x≤340 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点C可能是线段AB的中点 | |
| B. | 点D一定不是线段AB的中点 | |
| C. | 点C,D可能同时在线段AB上 | |
| D. | 点C,D可能同时在线段AB的延长线上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
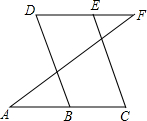 填写理由:如图所示
填写理由:如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
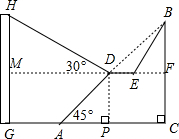 市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).
市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
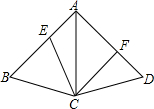 如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.
如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com