
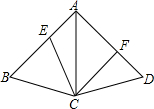
 如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.
如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半. 分析 分别作CG⊥AB与G,CH⊥AD与H,由AC为∠BAD的角平分线,得到CG=CH,根据等底等高的三角形的面积相等得到△ABC面积=△ACD面积,又由于AE=DF,得到△AEC面积=△CDF面积,于是△BCE面积=△ABC面积-△AEC面积,△BCE面积=△ACD面积-△CDF面积,求出△BCE面积=△ACF面积,由四边形AECF面积=△AEC面积+△ACF面积,四边形AECF面积=△AEC面积+△BCE面积,得到四边形AECF面积=△ABC面积,又由于四边形ABCD面积=△ABC面积+△ACD面积,四边形ABCD面积=2△ABC面积,即可得到结果.
解答 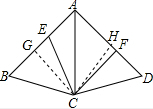 解:分别作CG⊥AB与G,CH⊥AD与H,
解:分别作CG⊥AB与G,CH⊥AD与H,
∵AC为∠BAD的角平分线,
∴CG=CH,
∵AB=AD,
∴△ABC面积=△ACD面积,
又∵AE=DF,
∴△AEC面积=△CDF面积,
∴△BCE面积=△ABC面积-△AEC面积,
△BCE面积=△ACD面积-△CDF面积,
∴△BCE面积=△ACF面积,
∵四边形AECF面积=△AEC面积+△ACF面积,
四边形AECF面积=△AEC面积+△BCE面积,
∴四边形AECF面积=△ABC面积,
又∵四边形ABCD面积=△ABC面积+△ACD面积,
又∵四边形ABCD面积=2△ABC面积,
∴四边形AECF面积为四边形ABCD面积的一半.
点评 本题考查了角平分线的性质,三角形的面积,正确的作出辅助线是解题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
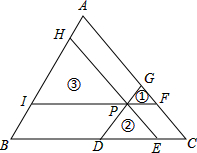 如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③.已知△ABC的面积的为36,小三角形①、②面积分别为1、4,则小三角形③的面积为9.
如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③.已知△ABC的面积的为36,小三角形①、②面积分别为1、4,则小三角形③的面积为9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:| A. | 两人皆正确 | B. | 两人皆错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3-x=x(x-1) | B. | x2-y2=(x-y)2 | ||
| C. | -4x2+9y2=(2x+3y)(2x-3y) | D. | x2+6x+9=(x+3)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com