
【题目】如图,![]() ,
,![]() 是射线
是射线![]() 上一点,以
上一点,以![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() ,使
,使![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() .
.
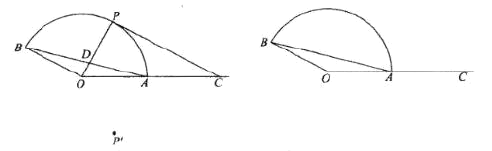
尝试: (1)点![]() 在
在![]() 所在的圆 (填“内”“上”或“外”);
所在的圆 (填“内”“上”或“外”);
(2)![]() .
.
发现 :(1)![]() 的最大值为 ;
的最大值为 ;
(2)当![]() ,
,![]() 时,判断
时,判断![]() 与
与![]() 所在圆的位置关系.
所在圆的位置关系.
探究:当点![]() 与
与![]() 的距离最大时,求
的距离最大时,求![]() 的长.(注:
的长.(注:![]() )
)
【答案】尝试:(1)上;(2)3;发现:(1)3;(2)相切,理由见解析;探究:![]()
【解析】
尝试:(1)根据题意即可得到结论;
(2)如图1,延长AO交![]() 所在圆上的点E,连接BE,根据等腰三角形的性质得到∠BAO=∠ABO=14°,根据三角函数的定义即可得到结论;
所在圆上的点E,连接BE,根据等腰三角形的性质得到∠BAO=∠ABO=14°,根据三角函数的定义即可得到结论;
发现:(1)在Rt△AOD中解直角三角形即可得到结论;
(2)根据弧长公式求得∠BOP=90°,根据切线的判定定理即可得到结论;
探究:作P′E⊥AB于点E,连接P′A,如图2,此时OE⊥AB,求得![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,
,![]() ,根据轴对称的性质即可得到AP=AP′=2
,根据轴对称的性质即可得到AP=AP′=2![]() .
.
尝试 (1)点P′在![]() 所在的圆上,
所在的圆上,
故答案为:上;
(2)如图1,延长AO交![]() 所在圆上的点E,
所在圆上的点E,
连接BE,
则∠ABE=90°,
∵∠AOB=152°,OB=OA,
∴∠BAO=∠ABO=14°,
∵OA=4,
∴AE=2OA=8,
∴AB=AEcos14°=8×![]() =2
=2![]() ,
,
故答案为:2![]() ;
;
发现 (1)当OP⊥AB时,PD有最大值,
在Rt△AOD中,∵OA=4,cos∠OAD=![]() ,
,

∴AD=![]() ,
,
∴OD=![]() =1,
=1,
∴PD=4-1=3,
∴PD的最大值为3,
故答案为:3;
(2)相切.
理由如下:
当![]() 时,
时,![]() .
.
解得![]() ,即
,即![]() .
.
∵![]() .
.
∴![]() .
.
又![]() ,∴
,∴![]() ,
,
∵![]() 是半径,
是半径,
∴![]() 与
与![]() 所在的圆相切.
所在的圆相切.
探究 作![]() 于点
于点![]() .
.
∵点![]() 在
在![]() 所在的圆上,∴当
所在的圆上,∴当![]() 过圆心
过圆心![]() 时,
时,![]() 最大.
最大.
连接![]() ,如图2.
,如图2.
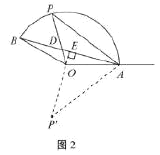
此时![]() .
.
![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
又点![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是( )
![]()
A. 45°B. 60°C. 75°D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,以BC为直径的半圆O交斜边AB于点 D.
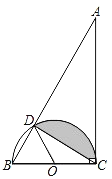
(1)证明:AD=3BD;
(2)求弧BD的长度;
(3)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
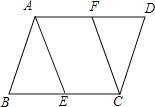
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com