
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,以BC为直径的半圆O交斜边AB于点 D.
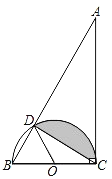
(1)证明:AD=3BD;
(2)求弧BD的长度;
(3)求阴影部分的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() ﹣
﹣![]()
【解析】
(1)根据直角三角形的性质以及圆周角和圆心角的性质求出∠COD=120°,结合圆的基本性质得出BC=2BD,再根据直角三角形中30°角的性质得出AB=2BC=4BD,即可得出答案;
(2)根据弧长公式即可得出答案;
(3)根据割补法结合扇形的面积公式计算即可得出答案.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,
∴∠COD=120°,
∵BC=4,BC为半圆O的直径,
∴∠CDB=90°,
∴∠BCD=30°,
∴BC=2BD,
∵∠A=30°,
∴AB=2BC=4BD,
∴AD=3BD;
(2)由(1)得∠B=60°,
∴OC=OD=OB=2,
∴弧BC的长为![]() ;
;
(3)∵BC=4,∠BCD=30°,
∴CD=![]() BC=
BC=![]() ,
,
图中阴影部分的面积=S扇形COD﹣S△COD=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知![]() 的三边长为
的三边长为![]() ,
,![]() ,
,![]() ,有以下三个结论:(1)以
,有以下三个结论:(1)以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;(2)以
为边长的三角形一定存在;(2)以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;(3)以
为边长的三角形一定存在;(3)以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在.其中正确结论的个数是( ).
为边长的三角形一定存在.其中正确结论的个数是( ).
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60°
(1)如图1,当点E是CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(2)如图2,当点E在CB的延长线上时,且∠EAB=15°,求点F到BC的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
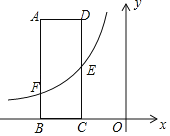
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,E是DC的中点,反比例函数y=![]() 的图象经过点E,与AB交于点F.
的图象经过点E,与AB交于点F.
(1)若点B坐标为(﹣6,0),求图象经过A、E两点的一次函数的表达式是_____;
(2)若AF﹣AE=2,则反比例函数的表达式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走52米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.大楼AB的高度约为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
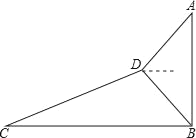
A. 32米B. 35米C. 36米D. 40米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.
(1)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.
(2)然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是射线
是射线![]() 上一点,以
上一点,以![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() ,使
,使![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() .
.
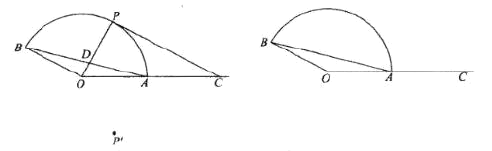
尝试: (1)点![]() 在
在![]() 所在的圆 (填“内”“上”或“外”);
所在的圆 (填“内”“上”或“外”);
(2)![]() .
.
发现 :(1)![]() 的最大值为 ;
的最大值为 ;
(2)当![]() ,
,![]() 时,判断
时,判断![]() 与
与![]() 所在圆的位置关系.
所在圆的位置关系.
探究:当点![]() 与
与![]() 的距离最大时,求
的距离最大时,求![]() 的长.(注:
的长.(注:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
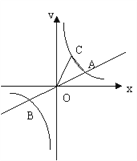
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,点B坐标为(-4,-2),C为双曲线
交于A、B两点,点B坐标为(-4,-2),C为双曲线![]() 上一点,且在第一象限内,若△AOC面积为6,则点C坐标为( )
上一点,且在第一象限内,若△AOC面积为6,则点C坐标为( )
A. (4,2) B. (2,3) C. (3,4) D. (2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com